题目内容
17.在正方体中ABCD-A1B1C1D1,若G点是△BA1D的重心,且$\overrightarrow{AG}$=x$\overrightarrow{AD}$+y$\overrightarrow{AB}$+z$\overrightarrow{C{C}_{1}}$,则x+y+z的值为( )| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
分析 利用空间向量加法法则求解.
解答 解:2$\overrightarrow{AO}$=$\overrightarrow{AB}+\overrightarrow{AD}$,$\overrightarrow{OG}=\frac{1}{3}\overrightarrow{OA}$,$\overrightarrow{O{A}_{1}}$=$\overrightarrow{OA}+\overrightarrow{A{A}_{1}}$,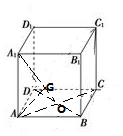
∴$\overrightarrow{AG}$=$\overrightarrow{AO}+\overrightarrow{OG}$
=$\overrightarrow{AO}+\frac{1}{3}\overrightarrow{O{A}_{1}}$
=$\overrightarrow{AO}+\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{A{A}_{1})}$
=$\frac{2}{3}\overrightarrow{AO}+\frac{1}{3}\overrightarrow{A{A}_{1}}$
=$\frac{1}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}+\frac{1}{3}\overrightarrow{C{C}_{1}}$,
∵$\overrightarrow{AG}$=x$\overrightarrow{AD}$+y$\overrightarrow{AB}$+z$\overrightarrow{C{C}_{1}}$,
∴x+y+z=$\frac{1}{3}+\frac{1}{3}+\frac{1}{3}$=1.
故选:B.
点评 本题考查代数式求和,是基础题,解题时要认真审题,注意空间向量加法法则的合理运用.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\overrightarrow{a}$=(0,0),$\overrightarrow{b}$=(1,-2) | B. | $\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(5,7) | C. | $\overrightarrow{a}$=(3,5),$\overrightarrow{b}$=(6,10) | D. | $\overrightarrow{a}$=(2,-3),$\overrightarrow{b}$=(4,-6) |
| A. | 24π | B. | 21 π | C. | 33π | D. | 39 π |