题目内容
14.若实数k满足0<k<9,则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1的( )| A. | 离心率相等 | B. | 虚半轴长相等 | C. | 实半轴长相等 | D. | 焦距相等 |
分析 根据k的取值范围,判断曲线为对应的双曲线,以及a,b,c的大小关系即可得到结论.
解答 解:当0<k<9,则0<9-k<9,16<25-k<25
曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1表示焦点在x轴上的双曲线,其中a2=25,b2=9-k,c2=34-k,
曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1表示焦点在x轴上的双曲线,其中a2=25-k,b2=9,c2=34-k,
即两个双曲线的焦距相等,
故选:D.
点评 本题主要考查双曲线的方程和性质,根据不等式的范围判断a,b,c是解决本题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
5.下列向量组中,能作为平面内所有向量的基底的是( )
| A. | $\overrightarrow{a}$=(0,0),$\overrightarrow{b}$=(1,-2) | B. | $\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(5,7) | C. | $\overrightarrow{a}$=(3,5),$\overrightarrow{b}$=(6,10) | D. | $\overrightarrow{a}$=(2,-3),$\overrightarrow{b}$=(4,-6) |
9.已知△ABC,AB=4,BC=3,AC=5,现以AB为轴旋转一周,则所得几何体的表面积( )
| A. | 24π | B. | 21 π | C. | 33π | D. | 39 π |
19.已知集合A={x|(3-x)(x+1)>0},B={x|-2<x≤1},则A∩B=( )
| A. | (-1,1] | B. | (-2,3] | C. | (-2,-1) | D. | (-2,1-)∪[1,3) |
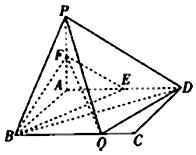 如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.
如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.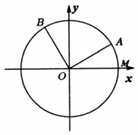 如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.
如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.