题目内容
12.设p:实数x,y满足(x-2)2+(y-2)2≤8,q:实数x,y满足$\left\{\begin{array}{l}y≥x-2\\ y≥2-x\\ y≤2\end{array}\right.$,则p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 画出(x-2)2+(y-2)2=8,和实数x,y满足$\left\{\begin{array}{l}y≥x-2\\ y≥2-x\\ y≤2\end{array}\right.$的区域根据充分条件和必要条件的定义分别进行判断即可.即可得答案.
解答 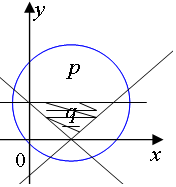 解:由题意:p:实数x,y满足(x-2)2+(y-2)2≤8的区域
解:由题意:p:实数x,y满足(x-2)2+(y-2)2≤8的区域
q:实数x,y满足$\left\{\begin{array}{l}y≥x-2\\ y≥2-x\\ y≤2\end{array}\right.$的区域,
如图所示:
从两个区域图不难看出:q推出P成立,而p推不出q一定成立.
∴p是q的必要不充分条件.
故选B.
点评 本题主要考查充分条件和必要条件的判断,利用到区域图,数形结合求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{A{A_1}}$=$\overrightarrow{c}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{BM}$可表示为( )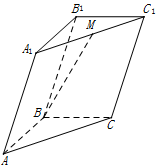

| A. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |
1.在下列区间中,函数f(x)=3x-2的零点所在的区间为( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
2.命题“若A=B,则A⊆B”与其逆命题、否命题、逆否命题这四个命题中,真命题的个数是( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
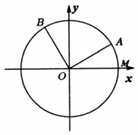 如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.
如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.