题目内容
若连续掷两次骰子，第一次掷得的点数为m，第二次掷得的点数为n，则点P（m，n）满足x2+y2＜16的概率是 ．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：本题是一个古典概型，试验发生的全部情况的总数为36，满足条件的事件可以通过列举得到，根据古典概型公式即可求解．
解答：
解：根据题意，本题是一个古典概型，
试验发生的全部情况的总数为6×6=36（种），
满足条件的事件有（1，1）（1，2）（1，3）（2，1）（2，2）（2，3）（3，1）（3，2），一共有8种结果，
点P（m，n）满足x2+y2＜16记为事件A，
∴P（A）=
=
．
故答案为：
．
试验发生的全部情况的总数为6×6=36（种），
满足条件的事件有（1，1）（1，2）（1，3）（2，1）（2，2）（2，3）（3，1）（3，2），一共有8种结果，
点P（m，n）满足x2+y2＜16记为事件A，
∴P（A）=
| 8 |
| 36 |
| 2 |
| 9 |
故答案为：
| 2 |
| 9 |
点评：本题主要考查了概率的运算，考查了学生的分析推理能力，解答此题的关键是要弄清楚两点：①符合条件的情况数目；②全部情况的总数；二者的比值就是其发生的概率的大小．
练习册系列答案
相关题目
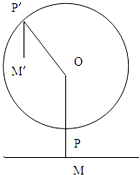六一儿重节到了，小明与爸爸去游乐场看见了大观览车，已知大观览车轮轴中心为点O，距地面高为32m（即OM=32m），巨轮半径为30m，点p为吊舱与轮的连接点，吊舱高2m（即PM=2m）巨轮每分钟转动30°，小明和爸爸从地面M点进入吊舱后，巨轮开始逆时针转动．