题目内容
求2x2+
的最小值.
| 1 |
| x2+1 |
考点:利用导数研究函数的单调性,基本不等式
专题:导数的综合应用
分析:令x2=t≥0,则2x2+
=2t+
=f(t),利用导数研究其单调性即可得出.
| 1 |
| x2+1 |
| 1 |
| t+1 |
解答:
解:令x2=t≥0,则2x2+
=2t+
=f(t),
则f′(t)=2-
=
>0,
因此函数f(t)在[0,+∞)单调递增,
∴当t=0即x=0时,函数f(t)取得最小值为1.
| 1 |
| x2+1 |
| 1 |
| t+1 |
则f′(t)=2-
| 1 |
| (t+1)2 |
| 2t2+4t+1 |
| (t+1)2 |
因此函数f(t)在[0,+∞)单调递增,
∴当t=0即x=0时,函数f(t)取得最小值为1.
点评:本题考查了利用导数研究函数的单调性极值与最值,属于基础题.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
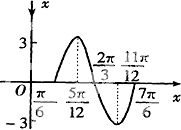 已知函数y=Asin(ωx+φ)(|φ|<
已知函数y=Asin(ωx+φ)(|φ|<