题目内容
20.已知函数f(x)=ax-1-lnx(a∈R).(1)讨论函数f(x)的单调区间;
(2)对任意a∈[1,4),且存在x∈[1,e3],使得不等式f(x)≥bx-2恒成立,求实数b的取值范围.
分析 (1)对函数进行求导,然后令导函数大于0求出x的范围,令导函数小于0求出x的范围,即可得到答案;
(2)问题转化为b≤a+$\frac{1-lnx}{x}$在[1,e3]恒成立,依据不等式恒成立时所取的条件,求出实数b的取值范围即可.
解答 解:(1)函数f(x)的定义域为(0,+∞)
.f′(x)=a-$\frac{1}{x}$=$\frac{ax-1}{x}$,
若a≤0,则f'(x)<0,
∴f(x)在(0,+∞)上递减;
若a>0,则由f'(x)>0得:x>$\frac{1}{a}$;
由f'(x)<0得:0<x<$\frac{1}{a}$
∴f(x)在(0,$\frac{1}{a}$)上递减,在($\frac{1}{a}$,+∞)递增.
(2)由f(x)≥bx-2得:b≤a+$\frac{1-lnx}{x}$,
令g(x)=a+$\frac{1-lnx}{x}$,
则g′(x)=$\frac{lnx-2}{{x}^{2}}$由g'(x)>0得:x>e2;
由g'(x)<0得:0<x<e2.
所以,g(x)在[1,e2)上递减,在(e2,e3]递增.
∴g(x)max=g(e3)=a-$\frac{2}{{e}^{3}}$,
∴b≤a-$\frac{2}{{e}^{3}}$,∵a∈[1,4),
∴b≤1-$\frac{2}{{e}^{3}}$.
点评 本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.已知0<c<1,a>b>1,下列不等式成立的是( )
| A. | ca>cb | B. | ac<bc | C. | $\frac{a}{a-c}>\frac{b}{b-c}$ | D. | logac>logbc |
8.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名五年级学生进行了问卷调查得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为$\frac{4}{15}$
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)若常喝碳酸饮料且肥胖的学生中有2名女生,现从常喝碳酸饮料且肥胖的学生中抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)若常喝碳酸饮料且肥胖的学生中有2名女生,现从常喝碳酸饮料且肥胖的学生中抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+x,x≤1}\\{lo{g}_{\frac{1}{3}}x,x>1}\end{array}\right.$,若对任意的x∈R,不等式f(x)≤$\frac{5}{4}$m-m2恒成立,则实数m的取值范围为( )
| A. | [-1,$\frac{1}{4}$] | B. | [$\frac{1}{4}$,1] | C. | [-2,$\frac{1}{4}$] | D. | [$\frac{1}{3}$,1] |
5.已知a,b∈R,定义运算“?”:a?b=$\left\{\begin{array}{l}{aa-b≤1}\\{ba-b>1}\end{array}\right.$,函数f(x)=(x2-2)?(x-1),x∈R,若方程f(x)-a=0只有两个不同实数根,则实数a的取值范围是( )
| A. | [-2,-1]∪(1,2) | B. | (-2,-1]∪(1,2] | C. | [-2,-1]∪[1,2] | D. | (-2,-1]∪(1,2) |
12.某程序如图所示,该程序运行后输出的最后一个数是( )
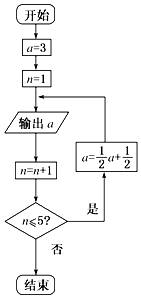

| A. | $\frac{17}{16}$ | B. | $\frac{9}{8}$ | C. | $\frac{5}{4}$ | D. | $\frac{3}{2}$ |
9.若直线x+y=0与圆x2+(y-a)2=1相切,则a的值为( )
| A. | 1 | B. | ±1 | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |
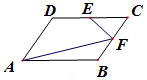 如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.
如图,菱形ABCD的边长为1,∠DAB=60°,E,F分别为DC、BC的中点,则$\overrightarrow{AF}•\overrightarrow{EF}$=$\frac{1}{8}$.