题目内容
9．若直线x+y=0与圆x2+（y-a）2=1相切，则a的值为（ ）| A． | 1 | B． | ±1 | C． | $\sqrt{2}$ | D． | ±$\sqrt{2}$ |
分析 由直线与圆相切，得到圆心到直线的距离等于圆的半径，利用点到直线的距离公式列出关于a的方程，求出方程的解即可得到a的值
解答 解：圆x2+（y-a）2=1的圆心坐标为（0，a），半径为1，
∵直线x+y=0与圆x2+（y-a）2=1相切，
∴圆心（0，a）到直线的距离d=r，
即$\frac{|a|}{\sqrt{2}}$=1，
解得：a=$±\sqrt{2}$．
故选D．
点评 本题考查了直线与圆的位置关系，当直线与圆相切时，圆心到直线的距离等于圆的半径，熟练掌握此性质是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
17．某四棱锥的三视图如图所示，则该四棱锥的底面的面积是（ ）
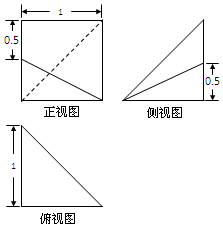
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
1．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$上任意一点P，作与y轴平行的直线，交两渐近线于A，B两点，若$\overrightarrow{PA}•\overrightarrow{PB}=-\frac{a^2}{4}$，则该双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{10}}}{3}$ | B． | $\sqrt{3}$ | C． | $\frac{{\sqrt{6}}}{2}$ | D． | $\frac{{\sqrt{5}}}{2}$ |
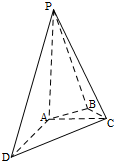如图，在四棱锥P-ABCD中，PA丄平面ABCD，AB丄BC，∠BCA=45°，PA=AD=2，AC=1，DC=$\sqrt{5}$