题目内容
8.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名五年级学生进行了问卷调查得到如下列联表(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)若常喝碳酸饮料且肥胖的学生中有2名女生,现从常喝碳酸饮料且肥胖的学生中抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)设常喝碳酸饮料肥胖的学生有x人,求出x的值,填表即可;
(2)计算观测值K2,对照数表得出结论;
(3)用列举法计算基本事件数,求出对应的概率值.
解答 解:(1)设常喝碳酸饮料肥胖的学生有x人,
则$\frac{x+2}{30}$=$\frac{4}{15}$,解得x=6;
填表如下;
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 6 | 2 | 8 |
| 不胖 | 4 | 18 | 22 |
| 合计 | 10 | 20 | 30 |
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关;
(3)设常喝碳酸饮料的肥胖者男生为A、B、C、D,女生为e、f,则任取两人有
AB,AC,AD,Ae,Af,BC,BD,Be,Bf,CD,Ce,Cf,De,Df,ef共15种.
其中一男一女有Ae,Af,Be,Bf,Ce,Cf,De,Df共8种;
故抽出一男一女的概率是P=$\frac{8}{15}$.
点评 本题考查了列联表与独立性检验的问题,也考查了等可能事件的概率问题,是基础题.

练习册系列答案
相关题目
16.已知抛物线y2=2px(p>0)过点A($\frac{1}{2}$,$\sqrt{2}$),其准线与x轴交于点B,直线AB与抛物线的另一个交点为M,若$\overrightarrow{MB}$=λ$\overrightarrow{AB}$,则实数λ为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
3.函数y=$\frac{1+x}{1-x}$的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
13.在区间[0,1]上随机选取两个数x和y,则y>3x的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{12}$ |
17.某四棱锥的三视图如图所示,则该四棱锥的底面的面积是( )
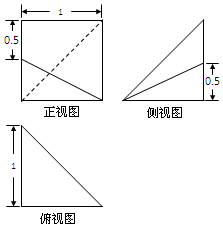

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
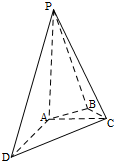 如图,在四棱锥P-ABCD中,PA丄平面ABCD,AB丄BC,∠BCA=45°,PA=AD=2,AC=1,DC=$\sqrt{5}$
如图,在四棱锥P-ABCD中,PA丄平面ABCD,AB丄BC,∠BCA=45°,PA=AD=2,AC=1,DC=$\sqrt{5}$