题目内容
10．已知0＜c＜1，a＞b＞1，下列不等式成立的是（ ）| A． | ca＞cb | B． | ac＜bc | C． | $\frac{a}{a-c}＞\frac{b}{b-c}$ | D． | logac＞logbc |
分析 根据题意，依次分析选项：对于A、构造函数y=cx，由指数函数的性质分析可得A错误，对于B、构造函数y=xc，由幂函数的性质分析可得B错误，对于C、由作差法比较可得C错误，对于D、由作差法利用对数函数的运算性质分析可得D正确，即可得答案．
解答 解：根据题意，依次分析选项：
对于A、构造函数y=cx，由于0＜c＜1，则函数y=cx是减函数，又由a＞b＞1，则有ca＞cb，故A错误；
对于B、构造函数y=xc，由于0＜c＜1，则函数y=xc是增函数，又由a＞b＞1，则有ac＞bc，故B错误；
对于C、$\frac{a}{a-c}$-$\frac{b}{b-c}$=$\frac{ab-ac-ab+bc}{（a-c）（b-c）}$=$\frac{c（b-a）}{（a-c）（b-c）}$，又由0＜c＜1，a＞b＞1，则（a-c）＞0、（b-c）＞0、（b-a）＜0，进而有$\frac{a}{a-c}$-$\frac{b}{b-c}$＜0，故有$\frac{a}{a-c}$＜$\frac{b}{b-c}$，故C错误；
对于D、logac-logbc=$\frac{lgc}{lga}$-$\frac{lgc}{lgb}$=lgc（$\frac{lgb-lga}{lga•lgb}$），又由0＜c＜1，a＞b＞1，则有lgc＜0，lga＞lgb＞0，则有logac-logbc=$\frac{lgc}{lga}$-$\frac{lgc}{lgb}$=lgc（$\frac{lgb-lga}{lga•lgb}$）＞0，即有logac＞logbc，故D正确；
故选：D．
点评 本题考查不等式比较大小，关键是掌握不等式的性质并灵活运用．
练习册系列答案
相关题目
20．已知曲线f（x）=ax-1+1（a＞1）恒过定点A，点A恰在双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线上，则双曲线C的离心率为（ ）
| A． | $\sqrt{5}$ | B． | 5 | C． | 2 | D． | 2$\sqrt{2}$ |
1．
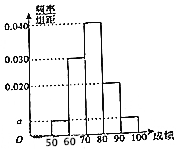某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计，绘制了频率分布直方图（如图所示）．规定80分及以上者晋级成功，否则晋级失败（满分100分）．
（Ⅰ）求图中a的值；
（Ⅱ）估计该次考试的平均分$\overline{x}$（同一组中的数据用该组的区间中点值代表）；
（Ⅲ）根据已知条件完成下面2×2列联表，并判断能否有85%的把握认为“晋级成功”与性别有关？
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
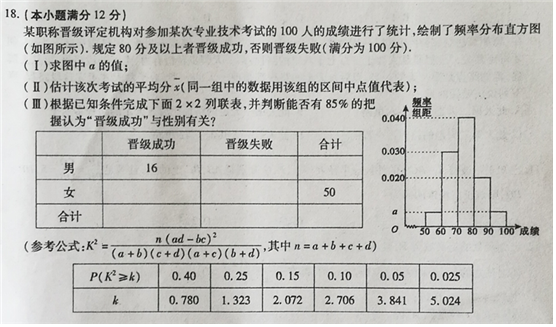
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计，绘制了频率分布直方图（如图所示）．规定80分及以上者晋级成功，否则晋级失败（满分100分）．（Ⅰ）求图中a的值；
（Ⅱ）估计该次考试的平均分$\overline{x}$（同一组中的数据用该组的区间中点值代表）；
（Ⅲ）根据已知条件完成下面2×2列联表，并判断能否有85%的把握认为“晋级成功”与性别有关？
| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P（K2≥k） | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
公元263年左右，我国数学家刘徽发现，当圆内接正多边形的边数无限增加时，正多边形的周长可无限逼近圆的周长，并创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的徽率，利用刘徽的割圆术设计的程序框图如图所示，若输出的n=96，则判断框内可以填入（ ）（参考数据：sin7.5°≈0.1305，sin3.75°≈0.06540，sin1.875°≈0.03272）