题目内容
计算1+
+
+…+
+
值的一个流程图是( )
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
| 1 |
| 102 |
A、 |
B、 |
C、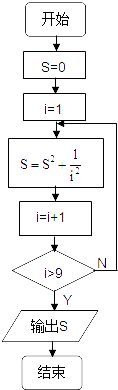 |
D、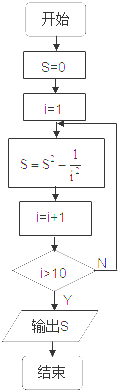 |
考点:程序框图
专题:常规题型,算法和程序框图
分析:对四个选项一一分析,注意循环体及跳出循环的条件.
解答:
解:选项A:计算1+
+
+…+
的值;
选项B:计算1+
+
+…+
+
的值,正确;
选项C、D:循环体中每一次求S是对上一个S求平方后加上
;故都不正确.
故选B.
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
选项B:计算1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
| 1 |
| 102 |
选项C、D:循环体中每一次求S是对上一个S求平方后加上
| 1 |
| i2 |
故选B.
点评:本题考查了读程序框图的能力,属于基础题.

练习册系列答案
相关题目
要得到y=sin(2x-
)的图象,需要将函数y=sin(2x+
)的图象( )
| π |
| 3 |
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知等差数列{an}中,a7+a9=30,a1=1,则a15=( )
| A、28 | B、29 | C、30 | D、31 |
设等差数列{an}{bn}的前n项和为Sn,Tn,若
=
,则
=( )
| Sn |
| Tn |
| n |
| n+1 |
| a5 |
| b7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线y=
在点(0,-1)处的切线方程为( )
| x+1 |
| x-1 |
| A、y=-2x-1 |
| B、y=2x-1 |
| C、y=-2x+1 |
| D、y=2x+1 |
设f(x)和g(x)是R上的奇函数,且g(x)≠0,当x<0时,f′(x)g(x)-f(x)g′(x)>0,且f(2)=0,则不等式
<0的解集是( )
| f(x) |
| g(x) |
| A、(-2,0)∪(2,+∞) |
| B、(-2,0)∪(0,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-2)∪(0,2) |
函数y=cosx+|cosx|x∈[0,2π]的大致图象为( )
A、 |
B、 |
C、 |
D、 |
下列求导运算正确的是( )
A、(x+
| ||||
| B、(3x)′=3xlog3e | ||||
C、(log3x)′=
| ||||
| D、(x2cosx)′=-2sinx |