题目内容
要得到y=sin（2x-
）的图象，需要将函数y=sin（2x+
）的图象（ ）
| π |
| 3 |
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：根据三角函数之间的关系即可得到结论．
解答：
解：∵y=sin（2x-
）=sin[2（x-
）+
]，
∴需要将函数y=sin（2x+
）的图象向右平移
个单位，即可，
故选：D
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴需要将函数y=sin（2x+
| π |
| 3 |
| π |
| 3 |
故选：D
点评：本题主要考查三角函数图象之间的关系，比较基础．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
下列函数中，值域为（0，+∞）的是（ ）
| A、y=log2x | ||
| B、y=x2-2x+1 | ||
C、y=（
| ||
| D、y=x-1 |
由x轴和y=2x2-x所围成的图形的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点M（x0，y0）是函数f（x）=2013sinx的图象上一点，且f（x0）=2013，则该函数图象在点M处的切线的斜率为（ ）
| A、2013 | B、-2013 |
| C、1 | D、0 |
已知A（2012，2013），B（2014，2015），则
=（ ）
| AB |
| A、（-2，2） |
| B、（2，-2） |
| C、（-2，-2） |
| D、（2，2） |
计算1+
+
+…+
+
值的一个流程图是（ ）
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
| 1 |
| 102 |
A、 |
B、 |
C、 |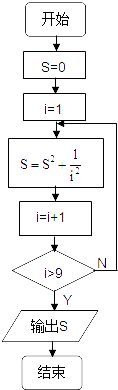
D、 |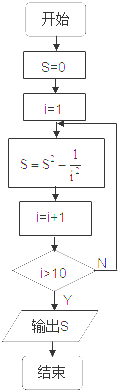
已知一个几何体的主视图及左视图均是边长为2的正三角形，俯视图是直径为2的圆，则此几何体的外接球的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|