题目内容
函数y=cosx+|cosx|x∈[0，2π]的大致图象为（ ）
A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：先去绝对值，化为分段函数，再根据余弦函数的单调性，得出答案．
解答：
解：y=cosx+|cosx|=
，
∵y=cosx在[0，
）为减函数，在（
，2π]为增函数，并且函数值都大于等于0，
只有D符合，
故选：D．
|
∵y=cosx在[0，
| π |
| 2 |
| 3π |
| 2 |
只有D符合，
故选：D．
点评：本题主要考查了分段函数的图象，以及余弦函数的图象，关键是化为分段函数，去绝对值，属于基础题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
下列函数中，值域为（0，+∞）的是（ ）
| A、y=log2x | ||
| B、y=x2-2x+1 | ||
C、y=（
| ||
| D、y=x-1 |
计算1+
+
+…+
+
值的一个流程图是（ ）
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
| 1 |
| 102 |
A、 |
B、 |
C、 |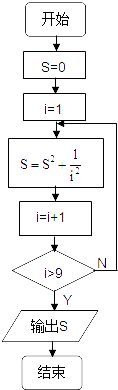
D、 |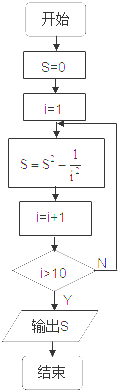
经过圆x2+2x+y2=0的圆心C，且与直线x+y=0平行的直线方程是 （ ）
| A、x+y+1=0 |
| B、x+y-1=0 |
| C、x-y+1=0 |
| D、x-y-1=0 |
已知（
-
）n的展开式中，第五项与第三项的二项式系数之比为14：3，则展开式的常数项是（ ）
| x |
| 2 |
| x2 |
| A、160 | B、80 |
| C、180 | D、64 |
已知一个几何体的主视图及左视图均是边长为2的正三角形，俯视图是直径为2的圆，则此几何体的外接球的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若a=log32，b=（
）-0.2，c=log
3，则a，b，c的大小关系为（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、b＞a＞c |
| B、a＞b＞c |
| C、c＞a＞b |
| D、a＞c＞b |
复数
等于（ ）
| 2 |
| 1+i |
| A、-2i | B、2i |
| C、1-i | D、1+i |