题目内容
设f(x)和g(x)是R上的奇函数,且g(x)≠0,当x<0时,f′(x)g(x)-f(x)g′(x)>0,且f(2)=0,则不等式
<0的解集是( )
| f(x) |
| g(x) |
| A、(-2,0)∪(2,+∞) |
| B、(-2,0)∪(0,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-2)∪(0,2) |
考点:函数奇偶性的性质
专题:导数的综合应用
分析:令h(x)=
,利用导数研究其单调性,再利用奇偶性即可得出.
| f(x) |
| g(x) |
解答:
解:当x∈(-∞,0)时,
令h(x)=
,则h′(x)=
>0,
∴函数h(x)在(-∞,0)上单调递增;
∵f(x)和g(x)是R上的奇函数,且g(x)≠0,
∴h(x)是R上的偶函数,
∴h(x)在(0,+∞)单调递减.
∵f(2)=0,
∴则不等式
<0的解集是(-∞,-2)∪(2,+∞).
故选:C.
令h(x)=
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
∴函数h(x)在(-∞,0)上单调递增;
∵f(x)和g(x)是R上的奇函数,且g(x)≠0,
∴h(x)是R上的偶函数,
∴h(x)在(0,+∞)单调递减.
∵f(2)=0,
∴则不等式
| f(x) |
| g(x) |
故选:C.
点评:本题考查了利用导数研究其单调性并解不等式、函数的奇偶性,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知A(2012,2013),B(2014,2015),则
=( )
| AB |
| A、(-2,2) |
| B、(2,-2) |
| C、(-2,-2) |
| D、(2,2) |
计算1+
+
+…+
+
值的一个流程图是( )
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
| 1 |
| 102 |
A、 |
B、 |
C、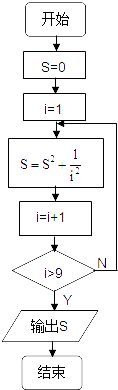 |
D、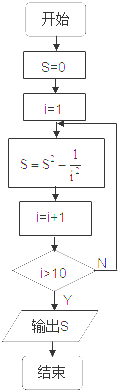 |
数列 0,0,0,…0…是( )
| A、是等差非等比数列 |
| B、是等比非等差数列 |
| C、既是等差又是等比 |
| D、非等差非等比 |
经过圆x2+2x+y2=0的圆心C,且与直线x+y=0平行的直线方程是 ( )
| A、x+y+1=0 |
| B、x+y-1=0 |
| C、x-y+1=0 |
| D、x-y-1=0 |
已知(
-
)n的展开式中,第五项与第三项的二项式系数之比为14:3,则展开式的常数项是( )
| x |
| 2 |
| x2 |
| A、160 | B、80 |
| C、180 | D、64 |
已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
直线
(t是参数)倾斜角为( )
|
| A、25° | B、65° |
| C、155° | D、115° |