题目内容
已知等差数列{an}中,a7+a9=30,a1=1,则a15=( )
| A、28 | B、29 | C、30 | D、31 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:利用等差数列的通项公式求解.
解答:
解:∵等差数列{an}中,a7+a9=30,a1=1,
∴1+6d+1+8d=30,
解得d=2,
∴a15=1+14×2=29.
故选:B.
∴1+6d+1+8d=30,
解得d=2,
∴a15=1+14×2=29.
故选:B.
点评:本题考查等差数列的第15项的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
下列函数中,值域为(0,+∞)的是( )
| A、y=log2x | ||
| B、y=x2-2x+1 | ||
C、y=(
| ||
| D、y=x-1 |
已知点M(x0,y0)是函数f(x)=2013sinx的图象上一点,且f(x0)=2013,则该函数图象在点M处的切线的斜率为( )
| A、2013 | B、-2013 |
| C、1 | D、0 |
已知A(2012,2013),B(2014,2015),则
=( )
| AB |
| A、(-2,2) |
| B、(2,-2) |
| C、(-2,-2) |
| D、(2,2) |
sin75°cos75°的值的符号( )
| A、大于0 | B、小于0 |
| C、大于等于0 | D、等于0 |
计算1+
+
+…+
+
值的一个流程图是( )
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
| 1 |
| 102 |
A、 |
B、 |
C、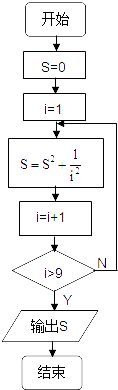 |
D、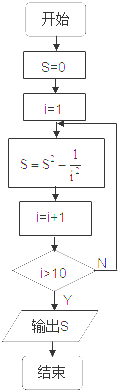 |
经过圆x2+2x+y2=0的圆心C,且与直线x+y=0平行的直线方程是 ( )
| A、x+y+1=0 |
| B、x+y-1=0 |
| C、x-y+1=0 |
| D、x-y-1=0 |
若a=log32,b=(
)-0.2,c=log
3,则a,b,c的大小关系为( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、b>a>c |
| B、a>b>c |
| C、c>a>b |
| D、a>c>b |