题目内容
曲线y=
在点（0，-1）处的切线方程为（ ）
| x+1 |
| x-1 |
| A、y=-2x-1 |
| B、y=2x-1 |
| C、y=-2x+1 |
| D、y=2x+1 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求函数的导数，因为函数在切点处的导数就是切线的斜率，求出斜率，再用点斜式写出切线方程，再化简即可．
解答：
解：y=
在的导数为y′=
=
，
∴曲线y=
在点（0，-1）处的切线斜率为-2，
切线方程是y+1=-2（x-0），
化简得，y=-2x-1
故选：A．
| x+1 |
| x-1 |
| x-1-(x+1) |
| (x-1)2 |
| -2 |
| (x-1)2 |
∴曲线y=
| x+1 |
| x-1 |
切线方程是y+1=-2（x-0），
化简得，y=-2x-1
故选：A．
点评：本题主要考查了函数的导数与切线斜率的关系，函数在某点处的导数即为曲线在该点处的切线的斜率，本题属于基础题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
已知点M（x0，y0）是函数f（x）=2013sinx的图象上一点，且f（x0）=2013，则该函数图象在点M处的切线的斜率为（ ）
| A、2013 | B、-2013 |
| C、1 | D、0 |
sin75°cos75°的值的符号（ ）
| A、大于0 | B、小于0 |
| C、大于等于0 | D、等于0 |
计算1+
+
+…+
+
值的一个流程图是（ ）
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
| 1 |
| 102 |
A、 |
B、 |
C、 |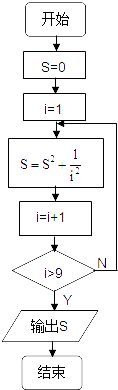
D、 |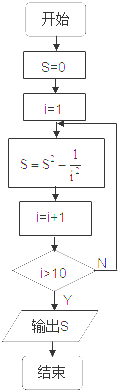
极坐标系中的点（2，0）到直线θ=
的距离是（ ）
| π |
| 4 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
经过圆x2+2x+y2=0的圆心C，且与直线x+y=0平行的直线方程是 （ ）
| A、x+y+1=0 |
| B、x+y-1=0 |
| C、x-y+1=0 |
| D、x-y-1=0 |
平面α，β的法向量分别是
=（1，1，1），
=（-1，0，-1），则平面α，β所成角的正弦值是（ ）
| n1 |
| n2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|