题目内容
设等差数列{an}{bn}的前n项和为Sn，Tn，若
=
，则
=（ ）
| Sn |
| Tn |
| n |
| n+1 |
| a5 |
| b7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：等差数列的性质
专题：等差数列与等比数列
分析：根据题意设Sn=kn2，Tn=kn（n+1），求出等差数列{an}，{bn}的通项，即可求值．
解答：
解：由题意得
=
，则设Sn=kn2，Tn=kn（n+1），
当n≥2时，an=Sn-Sn-1=2kn-k，n=1时也满足；
当n≥2时，bn=Tn-Tn-1=2kn，n=1时也满足，
所以
=
=
，
故选：B．
| Sn |
| Tn |
| n |
| n+1 |
当n≥2时，an=Sn-Sn-1=2kn-k，n=1时也满足；
当n≥2时，bn=Tn-Tn-1=2kn，n=1时也满足，
所以
| a5 |
| b7 |
| 10k-k |
| 14k |
| 9 |
| 14 |
故选：B．
点评：本题考查灵活运用等差数列的通项公式及前n项和的公式，本题的突破点是根据题意设出等差数列的前n项和的公式，并求出等差数列的通项公式．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
由x轴和y=2x2-x所围成的图形的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知A（2012，2013），B（2014，2015），则
=（ ）
| AB |
| A、（-2，2） |
| B、（2，-2） |
| C、（-2，-2） |
| D、（2，2） |
已知实数a，b∈{1，2，3}，则函数y=
x3-ax2+bx+5有极值的概率为（ ）
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
计算1+
+
+…+
+
值的一个流程图是（ ）
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 92 |
| 1 |
| 102 |
A、 |
B、 |
C、 |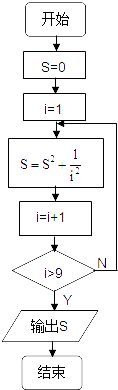
D、 |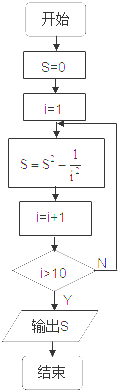
数列 0，0，0，…0…是（ ）
| A、是等差非等比数列 |
| B、是等比非等差数列 |
| C、既是等差又是等比 |
| D、非等差非等比 |
已知（
-
）n的展开式中，第五项与第三项的二项式系数之比为14：3，则展开式的常数项是（ ）
| x |
| 2 |
| x2 |
| A、160 | B、80 |
| C、180 | D、64 |
空间直角坐标系O-xyz中，点P（1，2，1）关于zOx平面的对称点是（ ）
| A、（1，-2，1） |
| B、（-1，-2，1） |
| C、（1，2，-1） |
| D、（-1，-2，-1） |