题目内容
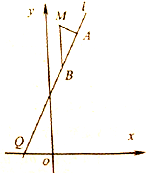 如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=
如图所示,已知一次函数y=kx+k的图象(直线l)与x轴交于点Q,M是二次函数y=| 1 |
| 2 |
| |QB|2 |
| |QA| |
考点:二次函数的性质
专题:函数的性质及应用
分析:设出点的坐标,分别表示出QB2,QA的长,得出
的比值,比较分子,分母,得出须使
=1,从而求出k的值.
| |QB|2 |
| |QA| |
| 2 |
| k |
解答:
解:y=kx+k=k(x+1),点Q(-1,0),
设M(x0,
(x02+x0)),QM2=(x0+1)2+
(x02+x0)2,
B(x0,k(x0+1)),A(x1,y1)
∴MA2=
,
QA=
=
,
QB2=(x0+1)2+k2(x0+1)2=(k2+1)(x0+1)2,
=
,
要使得
为常数,须使
=1,即k=2.
设M(x0,
| 1 |
| 2 |
| 1 |
| 4 |
B(x0,k(x0+1)),A(x1,y1)
∴MA2=
kx0-
| ||
| k2+1 |
QA=
| QM2-MA2 |
| ||
|
QB2=(x0+1)2+k2(x0+1)2=(k2+1)(x0+1)2,
| |QB|2 |
| |QA| |
2(k2+1)(x0+1)2
| ||
| |kx0+2||x0+1| |
要使得
| |QB|2 |
| |QA| |
| 2 |
| k |
点评:本题考查了二次函数的性质,考查了距离公式,计算量较大,是一道中档题.

练习册系列答案
相关题目
函数y=sin(2x+
)是( )
| 5π |
| 2 |
| A、周期为π的奇函数 | ||
| B、周期为π的偶函数 | ||
C、周期为
| ||
D、周期为
|
若f(x)=
,则f(
)•f(-100)=( )
|
| π |
| 4 |
| A、-2 | B、-1 | C、1 | D、2 |
已知p:
≤2x≤
,q:-
≤x+
≤-2,则p是q的( )
| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,在棱长为1的直三棱柱ABC-A1B1C1中,M为棱A1B1的中点,试求:
如图,在棱长为1的直三棱柱ABC-A1B1C1中,M为棱A1B1的中点,试求: