题目内容
已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)为偶函数,其图象上相邻的两个最高点间的距离为2π.
(1)求f(x)的解析式;
(2)α为锐角,且f(a+
)=
,求sin(
+α)的值.
(1)求f(x)的解析式;
(2)α为锐角,且f(a+
| π |
| 3 |
| 1 |
| 3 |
| 3π |
| 2 |
考点:正弦函数的图象,运用诱导公式化简求值
专题:三角函数的图像与性质
分析:(1)由周期求得ω,根据函数的奇偶性求得φ,可得函数的解析式.
(2)由f(a+
)=cos(α+
)=
,α为锐角,求得sin(α+
)的值,再根据sin(
+α)=-cosα=-cos[(α+
)-
],利用两角差的余弦公式计算求得结果.
(2)由f(a+
| π |
| 3 |
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 3 |
| π |
| 3 |
解答:
解:(1)∵图象上相邻的两个最高点间的距离为2π,∴T=
=2π,求得ω=1.
又f(x)为偶函数,则φ=kπ+
,k∈z,结合0≤φ≤π,可得φ=
,故f(x)=sin(x+
)=cosx.
(2)由f(a+
)=cos(α+
)=
,α为锐角,所以,sin(α+
)=
,
∴sin(
+α)=-cosα=-cos[(α+
)-
]=-[cos(α+
)cos
+sin(α+
)sin
]
=-[
×
+
×
]=-
.
| 2π |
| ω |
又f(x)为偶函数,则φ=kπ+
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(2)由f(a+
| π |
| 3 |
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
2
| ||
| 3 |
∴sin(
| 3π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=-[
| 1 |
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 2 |
2
| ||
| 6 |
点评:本题主要考查正弦函数的图象和性质,诱导公式、两角和差的余弦公式的应用,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若数列{an}的前n项和为Sn对任意正整数n都有Sn=2an-1,则S6=( )
| A、32 | B、31 | C、64 | D、63 |
cos(
-x)=
,那么sin2x=( )
| π |
| 4 |
| 3 |
| 5 |
A、
| ||
B、±
| ||
C、-
| ||
D、
|
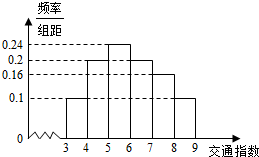 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从贵阳市交通指挥中心随机选取了二环以内50个交通路段,依据交通指数数据绘制的直方图如图所示:
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从贵阳市交通指挥中心随机选取了二环以内50个交通路段,依据交通指数数据绘制的直方图如图所示: