题目内容
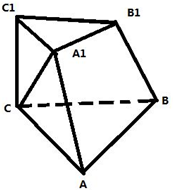 如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为
如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为| π |
| 3 |
考点:用空间向量求平面间的夹角
专题:计算题,空间角
分析:证明平面ABC⊥平面A1BC,∠A1BC是二面角A1-AB-C平面角,取BC的中点E,证明∠A1DE是二面角A1-AC-B的平面角,即可求出结论.
解答:
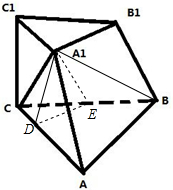 解:根据棱台性质可知,A1B1∥AB,A1B1⊥A1C(已知),∴AB⊥A1C,A1B1⊥B1C1,
解:根据棱台性质可知,A1B1∥AB,A1B1⊥A1C(已知),∴AB⊥A1C,A1B1⊥B1C1,
B1C1∥BC,AB∥A1B1,∴AB⊥BC,
∵A1C∩BC=C,AB⊥平面A1BC,
∵AB?平面ABC,∴平面ABC⊥平面A1BC.
由△A1BA是RT△,∠A1BA=90°,根据勾股定理,A1B=4.∠CBA=90°,BC=4,
∵A1B⊥AB,BC⊥AB,∴∠A1BC是二面角A1-AB-C平面角,∴∠A1BC=60°,
由三角形A1BC是等边三角形,S△A1BC=
•4•4sin60°=4
,
∴VC-A1BA=
S△A1BC•AB=4
.
取BC的中点E,△A1BC是等边三角形,A1E⊥BC,由前所述,平面ABC⊥平面A1BC,
∴A1E⊥平面ABC,E是A1在平面ABC的射影,
过E作ED⊥AB,根据三垂线定理可知A1D⊥AC,∠A1DE是二面角A1-AC-B的平面角,A1E=2
,
∵△CED∽△CAB,∴
=
,
∴DE=
,
∴tan∠A1DE=
=
,
∴tanθ=
.
 解:根据棱台性质可知,A1B1∥AB,A1B1⊥A1C(已知),∴AB⊥A1C,A1B1⊥B1C1,
解:根据棱台性质可知,A1B1∥AB,A1B1⊥A1C(已知),∴AB⊥A1C,A1B1⊥B1C1,B1C1∥BC,AB∥A1B1,∴AB⊥BC,
∵A1C∩BC=C,AB⊥平面A1BC,
∵AB?平面ABC,∴平面ABC⊥平面A1BC.
由△A1BA是RT△,∠A1BA=90°,根据勾股定理,A1B=4.∠CBA=90°,BC=4,
∵A1B⊥AB,BC⊥AB,∴∠A1BC是二面角A1-AB-C平面角,∴∠A1BC=60°,
由三角形A1BC是等边三角形,S△A1BC=
| 1 |
| 2 |
| 3 |
∴VC-A1BA=
| 1 |
| 3 |
| 3 |
取BC的中点E,△A1BC是等边三角形,A1E⊥BC,由前所述,平面ABC⊥平面A1BC,
∴A1E⊥平面ABC,E是A1在平面ABC的射影,
过E作ED⊥AB,根据三垂线定理可知A1D⊥AC,∠A1DE是二面角A1-AC-B的平面角,A1E=2
| 3 |
∵△CED∽△CAB,∴
| DE |
| AB |
| CE |
| AC |
∴DE=
| 6 |
| 5 |
∴tan∠A1DE=
2
| ||
|
5
| ||
| 3 |
∴tanθ=
5
| ||
| 3 |
点评:本题考查面面角,考查面面垂直,考查学生分析解决问题的能力,正确作出面面角是关键.

练习册系列答案
相关题目
下列函数在(1,+∞)为增函数的是( )
| A、y=x2-4x | ||
| B、y=|x-2| | ||
C、y=
| ||
| D、y=log0.5x |
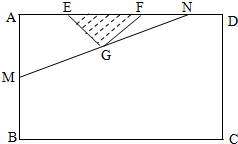 某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m).
某小区想利用一矩形空地ABCD建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中AD=60m,AB=40m,且△EFG中,∠EGF=90°,经测量得到AE=10m,EF=20m.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点G作一直线交AB,DF于M,N,从而得到五边形MBCDN的市民健身广场,设DN=x(m).