题目内容
已知f(x)的定义域为[-1,3],则f(x2)的定义域为 .
考点:函数的定义域及其求法
专题:转化思想,函数的性质及应用
分析:我们把f(x)的定义域为[-1,3]看作是一个大的条件,f(x2)看作是f(x)的一个特殊函数,那么f(x2)的定义域也要满足大条件[-1,3].
解答:
解:由f(x)的定义域为[-1,3],得:
-1≤x2≤3
解得:-
≤x≤
故答案为:[-
,
]
-1≤x2≤3
解得:-
| 3 |
| 3 |
故答案为:[-
| 3 |
| 3 |
点评:本题考察了定义域得求法,是一个基础题.做这类题关键是要注意取值范围是否扩大或者缩小,是闭区间还是开区间.

练习册系列答案
相关题目
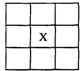 将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )
将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,一个空间几何体的正视图和侧视图都是边长为4的正方形,俯视图是一个圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和侧视图都是边长为4的正方形,俯视图是一个圆,那么这个几何体的体积为( )| A、12π | B、14π |
| C、16π | D、20π |
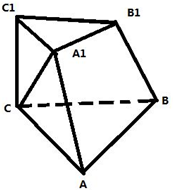 如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为
如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为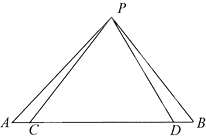 如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为
如图,C,D两点在△PAB的边AB上,AC=BD,若∠CPD=90°,且PA2+PB2=10,则2AB+CD的最大值为