题目内容
已知数列{an}的各项依次为a1=2,a2=22+23,a3=24+25+26,a4=27+28+29+210,…,则它的前n项和Sn= .
考点:数列的求和
专题:等差数列与等比数列
分析:通过观察,易发现数列的前n项和其实就是一个等比数列的求和,这题的关键点就在于能否准确的写出我们求的等比数列的项数.
解答:
解:由题意得:Sn=a1+a2+a3+…+an
=2+(22+23)+(24+25+26)+…+2
=2
-2
故答案为:2
-2
=2+(22+23)+(24+25+26)+…+2
| n(n+1) |
| 2 |
=2
| n2+n+2 |
| 2 |
故答案为:2
| n2+n+2 |
| 2 |
点评:对于数列得求和,我们首先要想到的是能不能转化为等差数列或者等比数列的求和,然后在考虑数列是不是周期数列,这也是解题时的一般思路.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知向量
=(2,1),
=(-3,4),则
-
的坐标为( )
| a |
| b |
| a |
| b |
| A、(-5,3) |
| B、(-1,5) |
| C、(5,-3) |
| D、(1,-5) |
数列{an}是首项为m、公比为q(q≠1)的等比数列,Sn是它的前n项和,对任意的n∈N,点(an,
)( )
| S2n |
| Sn |
| A、在直线mx+qy-q=0上 |
| B、在直线qx-my+m=0上 |
| C、在直线qx+my-q=0上 |
| D、不一定在一条直线上 |
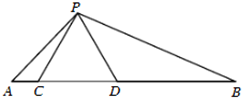 如图,点C、D在线段AB上,且△PCD是等边三角形.
如图,点C、D在线段AB上,且△PCD是等边三角形.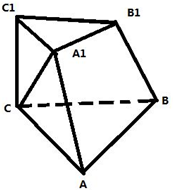 如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为
如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为