题目内容
下列函数在(1,+∞)为增函数的是( )
| A、y=x2-4x | ||
| B、y=|x-2| | ||
C、y=
| ||
| D、y=log0.5x |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据基本函数的性质,对每个函数分别判断即可.
解答:
解:由y=x2-4x=(x-2)2-4,得(2,+∞)是递增区间,
由y=|x-2|=
得(2,+∞)是递增区间,
y=
=-1-
在(1,+∞)上是递增函数,
y=log0.5x在(0,+∞)上是递减函数.
答案选C
由y=|x-2|=
|
y=
| x |
| 1-x |
| 1 |
| x-1 |
y=log0.5x在(0,+∞)上是递减函数.
答案选C
点评:本题考查基本初等函数的单调区间

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知向量
=(2,1),
=(-3,4),则
-
的坐标为( )
| a |
| b |
| a |
| b |
| A、(-5,3) |
| B、(-1,5) |
| C、(5,-3) |
| D、(1,-5) |
若直线ax-2y-1=0与直线x+y-2=0互相垂直,则a的值为( )
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
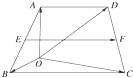 如图,在梯形ABCD中,AD∥BC,
如图,在梯形ABCD中,AD∥BC,| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| d |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
 如图所示,一个空间几何体的正视图和侧视图都是边长为4的正方形,俯视图是一个圆,那么这个几何体的体积为( )
如图所示,一个空间几何体的正视图和侧视图都是边长为4的正方形,俯视图是一个圆,那么这个几何体的体积为( )| A、12π | B、14π |
| C、16π | D、20π |
数列{an}是首项为m、公比为q(q≠1)的等比数列,Sn是它的前n项和,对任意的n∈N,点(an,
)( )
| S2n |
| Sn |
| A、在直线mx+qy-q=0上 |
| B、在直线qx-my+m=0上 |
| C、在直线qx+my-q=0上 |
| D、不一定在一条直线上 |
已知a=log3
,b=(
)-2,c=(
)3,则a,b,c的大小顺序为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、b<c<a |
| B、b<a<c |
| C、a<c<b |
| D、c<a<b |
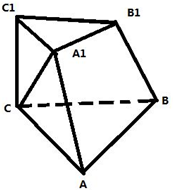 如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为
如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为