题目内容
已知数列{an}中,an=
,则前n项和Sn= .
|
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件知a2k-1=22k-2=4k-1,a2k=2(2k)-1=4k-1,由此利用分类讨论思想能求出结果.
解答:
解:∵数列{an}中,an=
,
∴a2k-1=22k-2=4k-1,
a2k=2(2k)-1=4k-1,
∴S2k=a1+a3+…+a2k-1+a2+a4+…+a2k
=40+4+…+4k-1+4(1+2+…+k)-k
=
+4×
-k
=
+2k2+k.
S2k-1=a1+a3+…+a2k-1+a2+a4+…+a2k-2
=40+4+…+4k-1+4[1+2+…+(k-1)]-(k-1)
=
+4×
-k+1
=
+2k2-3k+1.
∴Sn=
.
故答案为:
.
|
∴a2k-1=22k-2=4k-1,
a2k=2(2k)-1=4k-1,
∴S2k=a1+a3+…+a2k-1+a2+a4+…+a2k
=40+4+…+4k-1+4(1+2+…+k)-k
=
| 1-4k |
| 1-4 |
| k(k+1) |
| 2 |
=
| 4k-1 |
| 3 |
S2k-1=a1+a3+…+a2k-1+a2+a4+…+a2k-2
=40+4+…+4k-1+4[1+2+…+(k-1)]-(k-1)
=
| 1-4k |
| 1-4 |
| k(k-1) |
| 2 |
=
| 4k-1 |
| 3 |
∴Sn=
|
故答案为:
|
点评:本题考查数列的前n项和的求法,解题时要认真审题,注意分类讨论思想的合理运用,是一道比较难的题.

练习册系列答案
相关题目
已知向量
=(2,1),
=(-3,4),则
-
的坐标为( )
| a |
| b |
| a |
| b |
| A、(-5,3) |
| B、(-1,5) |
| C、(5,-3) |
| D、(1,-5) |
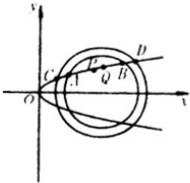 如图所示,设抛物线y2=2px,(0<p<1)与圆(x-5)2+y2=9在x轴上方的交点为A、B,与圆(x-6)2+y2=27在x轴上方的交点为C、D,P为AB中点,Q为CD的中点.
如图所示,设抛物线y2=2px,(0<p<1)与圆(x-5)2+y2=9在x轴上方的交点为A、B,与圆(x-6)2+y2=27在x轴上方的交点为C、D,P为AB中点,Q为CD的中点.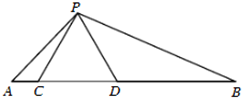 如图,点C、D在线段AB上,且△PCD是等边三角形.
如图,点C、D在线段AB上,且△PCD是等边三角形.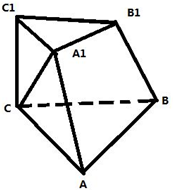 如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为
如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为