题目内容
在△ABC中,内角A、B、C所对的边分别为a、b、c,已知8b=5c,C=2B,则
的值为 .
| a2+b2-c2 |
| 2ab |
考点:余弦定理的应用
专题:计算题,解三角形
分析:利用8b=5c,C=2B,求出cosB=
,sinB=
,可得sinC,即可求出
的值.
| 4 |
| 5 |
| 3 |
| 5 |
| a2+b2-c2 |
| 2ab |
解答:
解:∵8b=5c,
∴8sinB=5sinC,
∵C=2B,
∴sinC=sin2B=2sinBcosB,
∴8sinB=10sinBcosB,
∴cosB=
,
∴sinB=
,
∴sinC=2sinBcosB=2×
×
=
,
∴cosC=
,
∴
=cosC=
,
故答案为:
.
∴8sinB=5sinC,
∵C=2B,
∴sinC=sin2B=2sinBcosB,
∴8sinB=10sinBcosB,
∴cosB=
| 4 |
| 5 |
∴sinB=
| 3 |
| 5 |
∴sinC=2sinBcosB=2×
| 4 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |
∴cosC=
| 7 |
| 25 |
∴
| a2+b2-c2 |
| 2ab |
| 7 |
| 25 |
故答案为:
| 7 |
| 25 |
点评:本题考查正弦定理、余弦定理,考查二倍角公式的运用,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
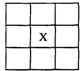 将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )
将1,1,2,2,2,3,3,3,3分别填入9个小方格中,每个小方格只填入一个数,每个数填入任何一个小方格是等可能的,则“3”填入图中标有“X”的小方格的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(2,1),
=(-3,4),则
-
的坐标为( )
| a |
| b |
| a |
| b |
| A、(-5,3) |
| B、(-1,5) |
| C、(5,-3) |
| D、(1,-5) |
若直线ax-2y-1=0与直线x+y-2=0互相垂直,则a的值为( )
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
已知a=log3
,b=(
)-2,c=(
)3,则a,b,c的大小顺序为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、b<c<a |
| B、b<a<c |
| C、a<c<b |
| D、c<a<b |
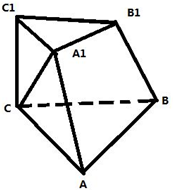 如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为
如图,在三棱台ABC-A1B1C1中,A1B1⊥A1C,A1B1⊥B1C1,AB=3,A1A=AC=5,二面角A1-AB-C大小为