题目内容
下列函数为奇函数的是( )
A、y=x
| ||
| B、y=lgx2 | ||
| C、1og2x | ||
D、y=2x-
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性的定义,对各个选项中的函数依次求出定义域,判断是否关于原点对称,若不关于原点对称则不是奇函数,否则再求出f(-x)化简判断与f(x)的关系,即可得答案.
解答:
解:对于A、函数y=x
的定义域是[0,+∞),不关于原点对称,所以不是奇函数,A错误;
对于B、函数y=lgx2的定义域是{x|x≠0},满足f(-x)=f(x),所以是偶函数,B错误;
对于C、函数y=1og2x的定义域是(0,+∞),不关于原点对称,所以不是奇函数,C错误;
对于D、函数y=2x-
的定义域是R,f(-x)=2-x-
=
-2x=-f(x),所以是奇函数,D正确,
故选:D.
| 1 |
| 2 |
对于B、函数y=lgx2的定义域是{x|x≠0},满足f(-x)=f(x),所以是偶函数,B错误;
对于C、函数y=1og2x的定义域是(0,+∞),不关于原点对称,所以不是奇函数,C错误;
对于D、函数y=2x-
| 1 |
| 2x |
| 1 |
| 2-x |
| 1 |
| 2x |
故选:D.
点评:本题考查利用函数奇偶性的定义判断函数的奇偶性,注意应先求出函数的定义域判断是否关于原点对称.

练习册系列答案
相关题目
定义max{a,b}=
,设实数x,y满足约束条件
,且z=max{3x+y,2x-y},则z的取值范围为( )
|
|
A、[-
| ||
| B、[-4,6] | ||
| C、[-8,7] | ||
| D、[-4,7] |
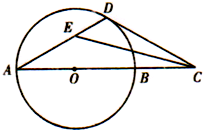 如图所示,在圆的直径AB的延长线上任取一点C,过点C作圆的切线CD,切点为D,∠ACD的平分线交AD于点E,则∠CED
如图所示,在圆的直径AB的延长线上任取一点C,过点C作圆的切线CD,切点为D,∠ACD的平分线交AD于点E,则∠CED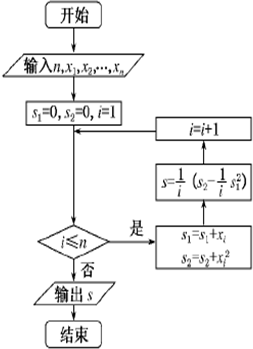 1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )