题目内容
3.执行如图所示的程序框图,则输出的结果是( )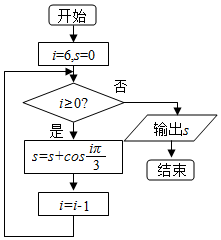
| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
分析 模拟执行该程序框图,得出程序输出的是计算S的值,分析最后一次循环情况,即可得出输出S的值.
解答 解:执行如图所示的程序框图,得:
该程序输出的是计算S的值;
当i=0时,满足条件,计算S=cos$\frac{6π}{3}$+cos$\frac{5π}{3}$+cos$\frac{4π}{3}$+cos$\frac{3π}{3}$+cos$\frac{2π}{3}$+cos$\frac{π}{3}$+cos0=1,
当i=-1时,不满足条件,输出S=1.
故选:D.
点评 本题考查了程序框图的应用问题,解题的关键是分析最后一次循环过程,是基础题目.

练习册系列答案
相关题目
14.执行如图所示的程序框图,如果输出的S=$\frac{1}{15}$,那么判断框内应填入的条件是( )

| A. | i<3 | B. | i<4 | C. | i<5 | D. | i<6 |
8.已知向量$\overrightarrow{a}$=(sinα,$\frac{3}{4}$),$\overrightarrow{b}$=(cosα,$\frac{\sqrt{3}}{4}$),α∈(0,π),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则α=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
15.已知双曲线的中心在原点,焦点在坐标轴上,一条渐近线方程为3x+4y=0,则该双曲线的离心率是( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$或$\frac{5}{3}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
