题目内容
15.已知双曲线的中心在原点,焦点在坐标轴上,一条渐近线方程为3x+4y=0,则该双曲线的离心率是( )| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$或$\frac{5}{3}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
分析 根据双曲线的渐近线的方程,讨论焦点在x轴,y轴上,结合离心率的定义进行求解即可.
解答 解:∵双曲线的一条渐近线方程为3x+4y=0,即y=-$\frac{3}{4}$x,
∴①若焦点在x轴,则$\frac{b}{a}$=$\frac{3}{4}$,
则离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+(\frac{b}{a})^{2}}$=$\sqrt{1+\frac{9}{16}}=\sqrt{\frac{25}{16}}$=$\frac{5}{4}$,
②若焦点在y轴,则$\frac{a}{b}$=$\frac{3}{4}$,即$\frac{b}{a}$=$\frac{4}{3}$
则离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+(\frac{b}{a})^{2}}$=$\sqrt{1+\frac{16}{9}}$=$\sqrt{\frac{25}{9}}$=$\frac{5}{3}$,
则双曲线的离心率e=$\frac{5}{3}$或$\frac{5}{4}$,
故选:D.
点评 本题主要考查双曲线离心率的计算,根据双曲线渐近线的方程结合双曲线离心率的定义是解决本题的关键.考查学生的转化能力.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
6.如果f(a+b)=f(a)•f(b)(a,b∈R),且f(1)=2,则$\frac{f(2)}{f(1)}$+$\frac{f(3)}{f(2)}$+$\frac{f(4)}{f(3)}$+…+$\frac{f(2015)}{f(2014)}$=( )
| A. | 4026 | B. | 4028 | C. | 2013 | D. | 2014 |
3.执行如图所示的程序框图,则输出的结果是( )
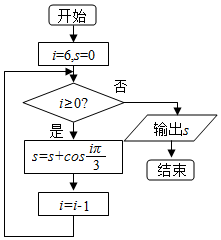

| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
7.若x,y都是区间[0,$\frac{π}{2}$]内任取的实数,则使得y<cosx的取值的概率是( )
| A. | $\frac{4}{{π}^{2}}$ | B. | $\frac{2}{π}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{{π}^{2}}$ |
4.若集合{x|y=ln(1-x2)},N={y|y=2x},则M∩N=( )
| A. | ∅ | B. | M | C. | N | D. | {x|0<x<1} |