题目内容
13．设奇函数f（x）满足3f（-2）=8+f（2），则f（-2）的值为-2．分析 由已知条件利用奇函数的性质得-3f（2）=8+f（2），由此f（-2）的值．
解答 解：∵奇函数f（x）满足3f（-2）=8+f（2），
∴-3f（2）=8+f（2），
∴4f（2）=-8，
解得f（2）=-2．
故答案为：-2．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意奇函数性质的合理运用．
练习册系列答案
天天练口算系列答案
相关题目
3．执行如图所示的程序框图，则输出的结果是（ ）
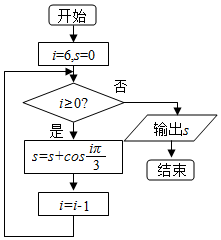
| A． | $-\frac{1}{2}$ | B． | 0 | C． | $\frac{1}{2}$ | D． | 1 |
4．若集合{x|y=ln（1-x2）}，N={y|y=2x}，则M∩N=（ ）
| A． | ∅ | B． | M | C． | N | D． | {x|0＜x＜1} |
1．已知集M={x|-2≤x≤6}，N={x|0≤2-x≤1}，在集合M中任取一个元素x，则x∈M∩N的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{8}$ |
8．
运行如图所示的程序框图，则输出S的值为（ ）
运行如图所示的程序框图，则输出S的值为（ ）| A． | -3 | B． | -2 | C． | 4 | D． | 8 |
18．已知集合A={x|x2-x-2≤0}，集合B={x|1＜x≤3}，则（∁RA）∩B=（ ）
| A． | （-1，1） | B． | （1，3] | C． | （2，3） | D． | （2，3] |
2．
执行如图的程序框图，若输入n为4，则输入S值为（ ）
执行如图的程序框图，若输入n为4，则输入S值为（ ）| A． | -10 | B． | -11 | C． | -21 | D． | 6 |