题目内容
14.已知函数f(x)=x2+1,g(x)=lg(2x-1),求f(2x-1),f(g(x)),g(f(x)).分析 直接代入即可求出f(2x-1),f(g(x)),g(f(x)).
解答 解:∵f(x)=x2+1,g(x)=lg(2x-1),
∴f(2x-1)=(2x-1)2+1=4x2-4x+2,
∴f(g(x))=g2(x)+1=lg2(2x-1)+1,
∴g(f(x))=lg[2f(x)-1]=lg[2(x2+1)-1]=lg(2x2+1).
点评 本题考查了函数的解析式的求法,属于基础题.

练习册系列答案
相关题目
3.执行如图所示的程序框图,则输出的结果是( )
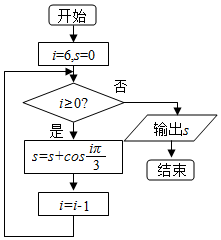

| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |