题目内容
8.已知向量$\overrightarrow{a}$=(sinα,$\frac{3}{4}$),$\overrightarrow{b}$=(cosα,$\frac{\sqrt{3}}{4}$),α∈(0,π),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则α=( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
分析 利用向量共线列出方程,然后求解即可.
解答 解:向量$\overrightarrow{a}$=(sinα,$\frac{3}{4}$),$\overrightarrow{b}$=(cosα,$\frac{\sqrt{3}}{4}$),α∈(0,π),且$\overrightarrow{a}$∥$\overrightarrow{b}$,
可得:$\frac{3}{4}$cosα=$\frac{\sqrt{3}}{4}$sinα,
即tanα=$\sqrt{3}$,
α=$\frac{π}{3}$.
故选:C.
点评 本题考查三角函数的化简求值,向量共线的充要条件,考查计算能力.

练习册系列答案
相关题目
19.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴为A1A2,虚轴的一个端点为B,若三角形A1A2B的面积为$\sqrt{2}$b2,则双曲线的离心率( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
3.执行如图所示的程序框图,则输出的结果是( )
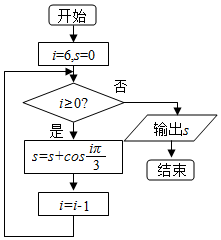

| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
13.复数z=$\frac{2+i}{1-2i}$的虚部为( )
| A. | -$\frac{5}{3}$ | B. | -$\frac{5}{3}$i | C. | 1 | D. | i |
18.已知集合A={x|x2-x-2≤0},集合B={x|1<x≤3},则(∁RA)∩B=( )
| A. | (-1,1) | B. | (1,3] | C. | (2,3) | D. | (2,3] |