题目内容
11.若变量x,y满足约束条件$\left\{{\begin{array}{l}{4x+3y-25≤0}\\{x-2y+2≤0}\\{x-1≥0}\end{array}}\right.$,则$\sqrt{{x^2}+{y^2}}$的最大值为5$\sqrt{2}$.分析 画出x、y满足约束条件可行域,目标函数则$\sqrt{{x^2}+{y^2}}$是可行域中的点(x,y)到原点的距离,利用线性规划进行求解.
解答  解:变量x,y满足约束条件$\left\{{\begin{array}{l}{4x+3y-25≤0}\\{x-2y+2≤0}\\{x-1≥0}\end{array}}\right.$,作出可行域,如图:
解:变量x,y满足约束条件$\left\{{\begin{array}{l}{4x+3y-25≤0}\\{x-2y+2≤0}\\{x-1≥0}\end{array}}\right.$,作出可行域,如图:
则$\sqrt{{x^2}+{y^2}}$是点(x,y)到原点的距离,
故最大值为点C到原点的距离,由直线4x+3y=25于x=1的交点,可得C(1,7)
则$\sqrt{{x^2}+{y^2}}$的最大值为:$\sqrt{{1}^{2}+{7}^{2}}$=5$\sqrt{2}$.
故答案为:$5\sqrt{2}$.
点评 此题主要考查简单的线性规划问题,是一道中档题,要学会画图.考查转化思想以及计算能力.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴为A1A2,虚轴的一个端点为B,若三角形A1A2B的面积为$\sqrt{2}$b2,则双曲线的离心率( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
6.如果f(a+b)=f(a)•f(b)(a,b∈R),且f(1)=2,则$\frac{f(2)}{f(1)}$+$\frac{f(3)}{f(2)}$+$\frac{f(4)}{f(3)}$+…+$\frac{f(2015)}{f(2014)}$=( )
| A. | 4026 | B. | 4028 | C. | 2013 | D. | 2014 |
3.执行如图所示的程序框图,则输出的结果是( )
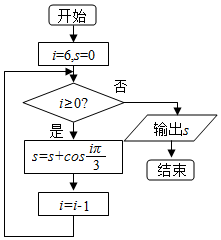

| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
1.已知集M={x|-2≤x≤6},N={x|0≤2-x≤1},在集合M中任取一个元素x,则x∈M∩N的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{8}$ |