题目内容
已知f(x)是定义在[-2,2]上的奇函数,且f(2)=3.若对任意的m,n∈[-2,2],m+n≠0,都有
>0.
(1)判断函数f(x)的单调性,并说明理由;
(2)若f(2a-1)<f(a2-2a+2),求实数a的取值范围;
(3)若不等式f(x)≤(5-2a)t+1对任意x∈[-2,2]和a∈[-1,2]都恒成立,求实数t的取值范围.
| f(m)+f(n) |
| m+n |
(1)判断函数f(x)的单调性,并说明理由;
(2)若f(2a-1)<f(a2-2a+2),求实数a的取值范围;
(3)若不等式f(x)≤(5-2a)t+1对任意x∈[-2,2]和a∈[-1,2]都恒成立,求实数t的取值范围.
考点:函数恒成立问题,函数单调性的判断与证明,函数单调性的性质
专题:计算题,压轴题,函数的性质及应用
分析:(1)设任意x1,x2,满足-2≤x1<x2≤2,利用函数单调性的定义证明;
(2)由(1)知,f(2a-1)<f(a2-2a+2)可化为-2≤2a-1)<a2-2a+2≤2,从而解得.
(3)不等式f(x)≤(5-2a)t+1对任意x∈[-2,2]和a∈[-1,2]都恒成立,fmax(x)≤(5-2a)t+1对任意的a∈[-1,2]都恒成立,令g(a)=2ta-5t+2,a∈[-1,2],从而求t.
(2)由(1)知,f(2a-1)<f(a2-2a+2)可化为-2≤2a-1)<a2-2a+2≤2,从而解得.
(3)不等式f(x)≤(5-2a)t+1对任意x∈[-2,2]和a∈[-1,2]都恒成立,fmax(x)≤(5-2a)t+1对任意的a∈[-1,2]都恒成立,令g(a)=2ta-5t+2,a∈[-1,2],从而求t.
解答:
解:(1)设任意x1,x2,满足-2≤x1<x2≤2,由题意可得
f(x1)-f(x2)=f(x1)+f(-x2)=
(x1-x2)<0,
即f(x1)<f(x2),
∴f(x)在定义域[-2,2]上是增函数.
(2)由(1)知,f(2a-1)<f(a2-2a+2)可化为
-2≤2a-1)<a2-2a+2≤2,
解得0≤a<1,
∴a的取值范围为[0,1).
(3)由(1)知,不等式f(x)≤(5-2a)t+1对任意x∈[-2,2]和a∈[-1,2]都恒成立,
fmax(x)≤(5-2a)t+1对任意的a∈[-1,2]都恒成立,
∴3≤(5-2a)t+1恒成立,
即2ta-5t+2≤0对任意的a∈[-1,2]都恒成立,
令g(a)=2ta-5t+2,a∈[-1,2],
则只需
,
解得t≥2,
∴t的取值范围是[2,+∞).
f(x1)-f(x2)=f(x1)+f(-x2)=
| f(x1)+f(-x2) |
| x1+(-x2) |
即f(x1)<f(x2),
∴f(x)在定义域[-2,2]上是增函数.
(2)由(1)知,f(2a-1)<f(a2-2a+2)可化为
-2≤2a-1)<a2-2a+2≤2,
解得0≤a<1,
∴a的取值范围为[0,1).
(3)由(1)知,不等式f(x)≤(5-2a)t+1对任意x∈[-2,2]和a∈[-1,2]都恒成立,
fmax(x)≤(5-2a)t+1对任意的a∈[-1,2]都恒成立,
∴3≤(5-2a)t+1恒成立,
即2ta-5t+2≤0对任意的a∈[-1,2]都恒成立,
令g(a)=2ta-5t+2,a∈[-1,2],
则只需
|
解得t≥2,
∴t的取值范围是[2,+∞).
点评:本题考查了函数的单调性的判断与证明,同时考查了单调性的应用及恒成立问题,属于难题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
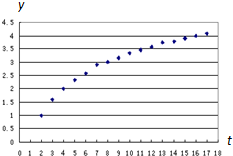 某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )
某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )| A、y=2t |
| B、y=2t2 |
| C、y=log2t |
| D、y=t3 |
数列{an}的通项为an=(-1)n•n•sin
+1前n项和为Sn,S100=( )
| nπ |
| 2 |
| A、50 | B、100 |
| C、-150 | D、150 |
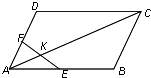 如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,
如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,