题目内容
在等差数列{an}中，a4=7，a1+a5=10，则公差d=（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：由等差数列的性质可得a3=5，易得公差d
解答：
解：由等差数列的性质可得a1+a5=2a3=10，
∴a3=5，又a4=7，∴公差d=7-5=2
故选：B
∴a3=5，又a4=7，∴公差d=7-5=2
故选：B
点评：本题考查等差数列的通项公式，涉及等差数列的性质，属基础题．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
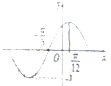函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0），|φ|≤| π |
| 2 |
A、f（x）=sin（2x+
| ||
B、f（x）=sin（2x-
| ||
C、f（x）=sin（4x+
| ||
D、f（x）=sin（4x-
|
设全集I={0，1，2，3，4，5}，集合A={0，1，2}，集合B={2，4，5}，则∁IA∪B=（ ）
| A、{4，5} |
| B、{0，1，2，3} |
| C、{2，3，4，5} |
| D、{0，1，2，3，4，5} |
下列各组函数表示相等函数的是 （ ）
A、f（x）=x+2与g（x）=
| |||||
| B、f（x）=（x-1）2与 g（x）=x-1 | |||||
C、f（x）=|x|与 g（x）=
| |||||
D、f（x）=
|