题目内容
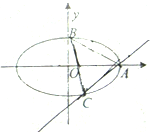 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| ||
| 2 |
(1)求椭圆的标准方程;
(2)过点A作斜率为k(k>0)的直线l与椭圆交于另外一点C,求△ABC面积的最大值,并求此时直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由于|AB|=
,离心率
.可得
=
,
=
,又a2=b2+c2,解得即可.
(2)由于kAB=-
=-
.设与直线AB平行的椭圆的切线为y=-
x+m.与椭圆的方程联立,利用△=0,可得m.解得切点C时,△ABC面积取得最大值,利用点到直线的距离公式可得点C到直线ABy=-
x+1的距离d,即可得到△ABC面积取得最大值=
•d•|AB|.计算此时直线l的斜率k即可得出直线l的方程.
| 5 |
| ||
| 2 |
| a2+b2 |
| 5 |
| c |
| a |
| ||
| 2 |
(2)由于kAB=-
| b |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵|AB|=
,离心率
.
∴
=
,
=
,
又a2=b2+c2,
解得c2=3,a2=4,b2=1.
∴椭圆的标准方程为
+y2=1.
(2)∵kAB=-
=-
.
设与直线AB平行的椭圆的切线为y=-
x+m.
联立
,化为2x2-4mx+4m2-4=0,(*)
∵△=16m2-4×2×(4m2-4)=0,
解得m=±
.
取m=-
,
则(*)化为:2x2+4
x+4=0,
解得x=-
,
代入y=-
x-
,可得y=-
.
∴当取C(-
,-
)时,△ABC面积取得最大值,
点C到直线ABy=-
x+1的距离d=
=
.
|AB|=
.
∴△ABC面积取得最大值=
×
×
=
+1.
此时直线l的斜率k=
=
.
∴直线l的方程为y=
(x-2),即y=
x+1-
.
| 5 |
| ||
| 2 |
∴
| a2+b2 |
| 5 |
| c |
| a |
| ||
| 2 |
又a2=b2+c2,
解得c2=3,a2=4,b2=1.
∴椭圆的标准方程为
| x2 |
| 4 |
(2)∵kAB=-
| b |
| a |
| 1 |
| 2 |
设与直线AB平行的椭圆的切线为y=-
| 1 |
| 2 |
联立
|
∵△=16m2-4×2×(4m2-4)=0,
解得m=±
| 2 |
取m=-
| 2 |
则(*)化为:2x2+4
| 2 |
解得x=-
| 2 |
代入y=-
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
∴当取C(-
| 2 |
| ||
| 2 |
点C到直线ABy=-
| 1 |
| 2 |
|-
| ||||||||
|
2
| ||||
| 5 |
|AB|=
| 5 |
∴△ABC面积取得最大值=
| 1 |
| 2 |
2
| ||||
| 5 |
| 5 |
| 2 |
此时直线l的斜率k=
| ||||
2+
|
| ||
| 2 |
∴直线l的方程为y=
| ||
| 2 |
| ||
| 2 |
| 2 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相切问题、点到直线的距离公式、三角形的面积计算公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
设全集I={0,1,2,3,4,5},集合A={0,1,2},集合B={2,4,5},则∁IA∪B=( )
| A、{4,5} |
| B、{0,1,2,3} |
| C、{2,3,4,5} |
| D、{0,1,2,3,4,5} |
如图,下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形序号是( )


| A、①② | B、③④ | C、②③ | D、①④ |
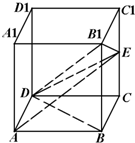 在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.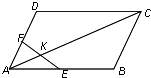 如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,
如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,