题目内容
12.{an}是等差数列,{bn}是等比数列,Tn是{bn}的前n项和,a1=b1=1,且满足$\sqrt{{a_2}+2}+\sqrt{{b_2}-2}=2\sqrt{2}$,当a2+b2取最小值时,(1)求Tn;
(2)Sn是{|an|}的前n项和,求Sn.
分析 利用柯西不等式(a2+2+b2-2)(1+1)≥($\sqrt{{a}_{2}+2}+\sqrt{{b}_{2}-2}$)2=8,可得(a2+b2)min=4,此时a2+2=b2-2,可得a2,b2,及等比数列{bn}的公比,等差数列{an}的公差
(1)直接用公式求Tn
(2)|a1|=1,n≥2时,|an|=n-2,再求Sn.
解答 解:利用柯西不等式(a2+2+b2-2)(1+1)≥($\sqrt{{a}_{2}+2}+\sqrt{{b}_{2}-2}$)2=8,
∴(a2+b2)min=4,此时a2+2=b2-2,a2=0,b2=4,
∴等比数列{bn}的公比为4,等差数列{an}的公差为-1
(1)Tn=$\frac{1×(1-{4}^{n})}{1-4}=\frac{1}{3}({4}^{n}-1)$
(2)|a1|=1,n≥2时,|an|=n-2,{|an|}的前n项和Sn,
Sn=$\left\{\begin{array}{l}{1\\;\\;(n=1)}\\{1+\frac{(n-1)(0+n-2)}{2}=\frac{{n}^{2}-3n+4}{2}\\;(n≥2)}\end{array}\right.$
点评 .本题考查了等差、等比数列的通项及性质,求和公式,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
20.已知x>-1,则$x+\frac{4}{x+1}$的最小值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
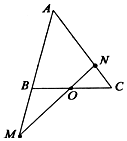 如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,则m+n的取值范围为[2,+∞).
如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,则m+n的取值范围为[2,+∞).