题目内容
17.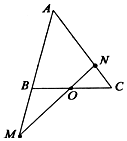 如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,则m+n的取值范围为[2,+∞).
如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,则m+n的取值范围为[2,+∞).
分析 由三点共线时,以任意点为起点,这三点为终点的三向量,其中一向量可用另外两向量线性表示,其系数和为1得到$\frac{1}{2m}$+$\frac{1}{2n}$=1,然后利用基本不等式求最值
解答 解:∵△ABC中,点O是BC的中点,
∴$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∵$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,
∴$\overrightarrow{AO}$=$\frac{1}{2m}$$\overrightarrow{AM}$+$\frac{1}{2n}$$\overrightarrow{AN}$,
又∵O,M,N三点共线,
∴$\frac{1}{2m}$+$\frac{1}{2n}$=1,
∴m+n=$\frac{1}{2}$(m+n)($\frac{1}{m}$+$\frac{1}{n}$)=$\frac{1}{2}$(2+$\frac{n}{m}$+$\frac{m}{n}$)≥$\frac{1}{2}$(2+2$\sqrt{\frac{m}{n}•\frac{n}{m}}$)=2,当且仅当m=n=1时取等号,
故m+n的取值范围为[2,+∞),
故答案为:[2,+∞)
点评 本题考查了共线向量基本定理的应用,考查了利用基本不等式求最值,关键是“1”的用法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.函数f(x)=loga|x+1|在(-1,0)上是增函数,则f(x)在(-∞,-1)上是( )
| A. | 函数值由负到正且为增函数 | B. | 函数值恒为正且为减函数 | ||
| C. | 函数值由正到负且为减函数 | D. | 没有单调性 |
5.设F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左右焦点,点P(x,y)在直线y-x-3=0上(x≠-3且$x≠±\sqrt{3}$),直线PF1,PF2的斜率分别为k1、k2,则$\frac{1}{k_2}-\frac{2}{k_1}$的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\sqrt{2}$ | D. | -1 |
9.已知椭圆$\frac{x^2}{5}$+$\frac{y^2}{m}$=1的离心率e=$\frac{{\sqrt{10}}}{5}$,则m的值为( )
| A. | 3 | B. | $\frac{25}{3}$或 3 | C. | $\sqrt{5}$ | D. | $\frac{{5\sqrt{15}}}{3}$或$\sqrt{15}$ |
 在正方体ABCD-A1B1C1D1中,E,F,G分别为A1B1,BB1,B1C1的中点,则AC1
在正方体ABCD-A1B1C1D1中,E,F,G分别为A1B1,BB1,B1C1的中点,则AC1