题目内容
7.-1,a1,a2,-4成等差数列,-1,b,-4成等比数列,则$\frac{{{a_2}+{a_1}}}{b}$=$±\frac{5}{2}$.分析 利用等差数列通项公式求出a2+a1,利用等比数列性质求出b,由此能求出结果.
解答 解:∵-1,a1,a2,-4成等差数列,
∴a2+a1=-1-4=-5,
∵-1,b,-4成等比数列,
∴b=$±\sqrt{(-1)×(-4)}$=±2,
∴$\frac{{{a_2}+{a_1}}}{b}$=$\frac{-5}{±2}$=$±\frac{5}{2}$.
故答案为:$±\frac{5}{2}$.
点评 本题考查代数式求和,是基础题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
相关题目
4.在棱锥P-ABC中,侧棱PA、PB、PC两两垂直,Q为底面△ABC内一点,若点Q到三个侧面的距离分别为3、4、5,则以线段PQ为直径的球的体积为( )
| A. | $\frac{125π}{6}$ | B. | $\frac{{125\sqrt{2}π}}{3}$ | C. | $\frac{50π}{3}$ | D. | $\frac{25π}{3}$ |
18.集合M={x|x2-x-6≥0},集合N={x|-3≤x≤1},则N∩(∁RM)等于( )
| A. | [-2,1] | B. | (-2,1] | C. | [-3,3) | D. | (-2,3) |
15.若${({X-2})^5}={a_5}{X^5}+{a_4}{X^4}+{a_3}{X^3}+{a_2}{X^2}+{a_1}X+{a_0}$,则a1+a2+a3+a4+a5=( )
| A. | -1 | B. | 31 | C. | -33 | D. | -31 |
2.等比数列{an}前四项和为1,前8项和为17,则它的公比为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 2或-1 |
16.三个数a=(-0.3)0,b=0.32,c=20.3的大小关系为( )
| A. | a<b<0 | B. | a<c<b | C. | b<c<a | D. | b<a<c |
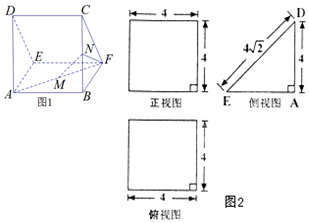 一个多面体的直观图(图1)及三视图(图2)如图所示,其中M、N分别是AF、BC的中点,
一个多面体的直观图(图1)及三视图(图2)如图所示,其中M、N分别是AF、BC的中点,