题目内容
2.已知数列{an}中,a1=2,an=2an-1-1,则通项an=2n-1+1.分析 推导出数列{an}是首项为1,公比为2的等比数列,由此能求出通项an.
解答 解:∵数列{an}中,a1=2,an=2an-1-1,
∴an-1=2(an-1-1),
∴$\frac{{a}_{n}-1}{{a}_{n-1}-1}$=2,a1-1=2-1=1,
∴数列{an}是首项为1,公比为2的等比数列,
∴an-1=2n-1,
∴通项an=2n-1+1.
故答案为:2n-1+1.
点评 本题考查数列的通项的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
13.设等比数列{an}的公比q=1,前n项和为Sn,则$\frac{{S}_{4}}{{a}_{2}}$=( )
| A. | 2 | B. | 4 | C. | $\frac{15}{2}$ | D. | $\frac{17}{2}$ |
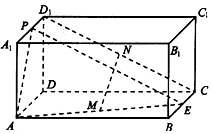 如图,在长方体ABCD-A1B1C1D1中,E、P分别是BC、A1D1的中点.M、N分别是AE、CD1的中点,AD=AA1=$\frac{1}{2}$AB=2.
如图,在长方体ABCD-A1B1C1D1中,E、P分别是BC、A1D1的中点.M、N分别是AE、CD1的中点,AD=AA1=$\frac{1}{2}$AB=2.