题目内容
为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者,从符合条件的200名志愿者中随机抽取60名志愿者,其中年龄分组区间是:[20,25),[25,30),[30,35),[35,40),[40,45]. 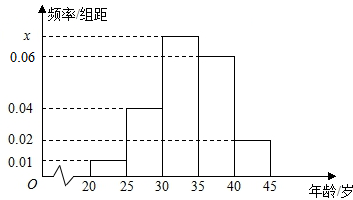
(1)求图中x的值并根据频率分布直方图估计这200名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的60名志愿者中按年龄在区间[20,35)和[35,45]采用分层抽样的方法抽取5名参加中心广场的宣传活动,再从这5名中采用简单随机抽样方法选取2名志愿者担任主要负责人,求所选两人中至少有一个年龄不低于35岁的概率.

(1)求图中x的值并根据频率分布直方图估计这200名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的60名志愿者中按年龄在区间[20,35)和[35,45]采用分层抽样的方法抽取5名参加中心广场的宣传活动,再从这5名中采用简单随机抽样方法选取2名志愿者担任主要负责人,求所选两人中至少有一个年龄不低于35岁的概率.
考点:分层抽样方法,频率分布直方图
专题:概率与统计
分析:(1)由频率分布直方图的性质,得x=
-0.01-0.02-0.04-0.06=0.07.由此求出这200名志愿者中年龄在[30,35)岁的频率,从而能求出这200名志愿者中年龄在[30,35)岁的人数.
(2)从这60人中采用分层抽样的方法抽取5名,则年龄在区间[20,35)内人数为:5×
=3,按年龄在区间[35,45]内人数为:5×
=2,由此能求出所选两人中至少有一个年龄不低于35岁的概率.
| 1 |
| 5 |
(2)从这60人中采用分层抽样的方法抽取5名,则年龄在区间[20,35)内人数为:5×
| 36 |
| 60 |
| 24 |
| 60 |
解答:
解:(1)由频率分布直方图的性质,得:
x=
-0.01-0.02-0.04-0.06=0.07.
这200名志愿者中年龄在[30,35)岁的频率为:0.07×5=0.35,
∴这200名志愿者中年龄在[30,35)岁的人数为:200×0.35=70(人).
(2)年龄在区间[20,35)内的人数为:(0.01+0.04+0.07)×5×200=120
年龄在区间[35,45]内的人数为:(0.06+0.02)×5×200=80,
∴在抽出的60名志愿者中按年龄在区间[20,35)内人数为:60×
=36,
按年龄在区间[35,45]内人数为:60×
=24,
从这60人中采用分层抽样的方法抽取5名,
则年龄在区间[20,35)内人数为:5×
=3,
按年龄在区间[35,45]内人数为:5×
=2,
∴所选两人中至少有一个年龄不低于35岁的概率:
p=1-
=0.7.
x=
| 1 |
| 5 |
这200名志愿者中年龄在[30,35)岁的频率为:0.07×5=0.35,
∴这200名志愿者中年龄在[30,35)岁的人数为:200×0.35=70(人).
(2)年龄在区间[20,35)内的人数为:(0.01+0.04+0.07)×5×200=120
年龄在区间[35,45]内的人数为:(0.06+0.02)×5×200=80,
∴在抽出的60名志愿者中按年龄在区间[20,35)内人数为:60×
| 120 |
| 200 |
按年龄在区间[35,45]内人数为:60×
| 80 |
| 200 |
从这60人中采用分层抽样的方法抽取5名,
则年龄在区间[20,35)内人数为:5×
| 36 |
| 60 |
按年龄在区间[35,45]内人数为:5×
| 24 |
| 60 |
∴所选两人中至少有一个年龄不低于35岁的概率:
p=1-
| ||
|
点评:本题考查分层抽样、频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意分层抽样性质的合理运用.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
定义符号函数sgn(x)=
,则下列结论中错误的是( )
|
| A、x=sgn(x)•|x| | ||
B、sgn(x)=
| ||
| C、sgn(x•y)=sgn(x)•sgn(y) | ||
| D、sgn(x+y)=sgn(x)+sgn(y) |
方程x2+
x-1=0的解可视为函数y=x+
的图象与函数y=
的图象交点的横坐标,若x4+ax-4=0的各个实根x1,x2,…,xk(k≤4)所对应的点(xi,
)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是( )
| 2 |
| 2 |
| 1 |
| x |
| 4 |
| xi |
| A、R |
| B、∅ |
| C、(-6,6) |
| D、(-∞,-6)∪(6,+∞) |