Question

方程x²+

2

x-1=0的解可视为函数y=x+

2

的图象与函数y=

1

x

的图象交点的横坐标，若x⁴+ax-4=0的各个实根x₁，x₂，…，x_k（k≤4）所对应的点（x_i，

4

xi

）（i=1，2，…，k）均在直线y=x的同侧，则实数a的取值范围是（　　）

• A、R
• B、∅
• C、（-6，6）
• D、（-∞，-6）∪（6，+∞）

Answer 1

考点：函数与方程的综合运用

专题：函数的性质及应用

分析：原方程等价于x³+a=

4

x

，分别作出y=x³+a与y=

4

x

的图象：分a＞0与a＜0讨论，数形结合即可．

解答： 解：方程的根显然不为0，原方程x⁴+ax-4=0等价于方程x³+a=

4

x

，
原方程的实根是曲线y=x³+a与曲线y=

4

x

的交点的横坐标；
曲线y=x³+a是由曲线y=x³向上或向下平移|a|个单位而得到的．
若交点（x_i，

4

xi

）（i=1，2，…，k）均在直线y=x的同侧，
则直线y=x与y=

4

x

的交点为：（-2，-2），（2，2）；
如下图所示：

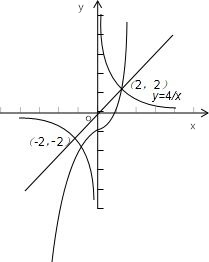
所以结合图象可得：

a＞0 x3+a＞-2 x≥-2

，
或

a＜0 x3+a＜2 x≤2

，
解得a＞6或a＜-6，
即实数a的取值范围是（-∞，-6）∪（6，∞），
故选D．

点评：本题考查函数与方程的综合运用，利用数形结合是解决本题的关键．注意合理地进行等价转化．