题目内容
设[x]表示不超过x的最大整数,如[1.4]=1,[-1.1]=-2,若函数f(x)=
,则函数g(x)=[f(x)]+[f(-x)]的值域为 .
| 1-ex |
| 1+ex |
考点:函数的值域
专题:新定义,函数的性质及应用
分析:分别求出函数f(x)和f(-x)的值域,利用[x]的定义,求[f(x)],[f(-x)]的值域,再相加.
解答:
解:∵f(x)=
=
-1,
∴当x>0时,1+ex>2,-1<f(x)<0,∴[f(x)]=-1;
当x<0时,1<1+ex<2,0<f(x)<1,∴[f(x)]=0;
当x=0时,f(x)=0,[f(x)]=0;
∵f(-x)=
=
=1-
,
∴当x>0时,1+ex>2,0<f(-x)<1,∴[f(x)]=0;
当x<0时,1<1+ex<2,-1<f(-x)<0,∴[f(x)]=-1;
当x=0时,f(-x)=0,[f(x)]=0;
综上,当x=0时,g(x)=[f(x)]+[f(-x)]=0,
当x>0时,g(x)=[f(x)]+[f(-x)]=-1+0=-1,
当x<0时,g(x)=[f(x)]+[f(-x)]=0-1=-1;
∴g(x)的值域是{0,-1}.
故答案为:{0,-1}.
| 1-ex |
| 1+ex |
| 2 |
| 1+ex |
∴当x>0时,1+ex>2,-1<f(x)<0,∴[f(x)]=-1;
当x<0时,1<1+ex<2,0<f(x)<1,∴[f(x)]=0;
当x=0时,f(x)=0,[f(x)]=0;
∵f(-x)=
| 1-e-x |
| 1+e-x |
| ex-1 |
| ex+1 |
| 2 |
| 1+ex |
∴当x>0时,1+ex>2,0<f(-x)<1,∴[f(x)]=0;
当x<0时,1<1+ex<2,-1<f(-x)<0,∴[f(x)]=-1;
当x=0时,f(-x)=0,[f(x)]=0;
综上,当x=0时,g(x)=[f(x)]+[f(-x)]=0,
当x>0时,g(x)=[f(x)]+[f(-x)]=-1+0=-1,
当x<0时,g(x)=[f(x)]+[f(-x)]=0-1=-1;
∴g(x)的值域是{0,-1}.
故答案为:{0,-1}.
点评:本题考查函数的新定义应用问题,解题时应深刻理解函数的新定义,利用指数函数的单调性求函数的值域,是解答问题的关键,是中档题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
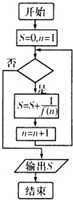
已知函数 f(x)=x2+x,执行如图所示的程序框图,若输出的结果是
,则判断框中的条件应是( )
| 31 |
| 32 |

| A、n≤30 | B、n≤31 |
| C、n≤32 | D、n≤33 |
下列说法正确的是( )
| A、命题“?x∈R,使得x2+x-1>0”的否定是“?x∈R,x2+x-1<0” | ||
B、命题p:“?x∈R,sinx+cosx≤
| ||
| C、“x=-1”是“x2-2x-3=0”的必要不充分条件 | ||
| D、“0<a<1”是“函数f(x)=ax(a>0,a≠1)在R上为减函数”的充要条件 |
