题目内容
如果点P在平面区域
上,点Q在曲线(x-1)2+y2=1上,那么|PQ|的最小值为 .
|
考点:简单线性规划
专题:不等式的解法及应用,直线与圆
分析:作出不等式组对应的平面区域,利用数形结合即可得到结论.
解答:
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由图象可知圆心D(1,0)到直线x-y+1=0的距离d=
=
=
,
由图象可知|PQ|的最小值为
-1,
故答案为:
-1
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:由图象可知圆心D(1,0)到直线x-y+1=0的距离d=
| |1-0+1| | ||
|
| 2 | ||
|
| 2 |
由图象可知|PQ|的最小值为
| 2 |
故答案为:
| 2 |
点评:本题主要考查线性规划的应用以及直线和圆的位置关系的应用,通过数形结合是解决本题的关键.

练习册系列答案
相关题目
等比数列{an}中,a3=16,a4=8,则a1=( )
| A、64 | B、32 | C、4 | D、2 |
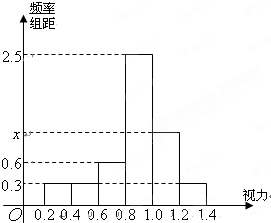 为了解某校高三学生的视力情况,随机抽查了该校50名高三学生,得到如图所示的频率分布直方图.
为了解某校高三学生的视力情况,随机抽查了该校50名高三学生,得到如图所示的频率分布直方图.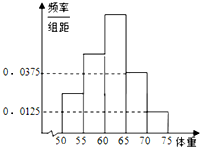 为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是
为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是