题目内容
已知函数f(x)=x2+
x-6.
(1)求函数g(x)=xf(x)的极大值;
(2)求过点A(2,-24)且与曲线y=x[f(x)-
x-6]相切的切线方程.
| 3 |
| 2 |
(1)求函数g(x)=xf(x)的极大值;
(2)求过点A(2,-24)且与曲线y=x[f(x)-
| 3 |
| 2 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:综合题,导数的概念及应用
分析:(1)求导数,确定函数的单调性,可求函数g(x)=xf(x)的极大值;
(2)设出曲线过点A切线方程的切点坐标,把切点的横坐标代入,可得切线的斜率,根据切点坐标和表示出的斜率,即可求出切线的方程.
(2)设出曲线过点A切线方程的切点坐标,把切点的横坐标代入,可得切线的斜率,根据切点坐标和表示出的斜率,即可求出切线的方程.
解答:
解:(1)g′(x)=[xf(x)]′=3(x-1)(x+2),
由g′(x)>0可得x<-2或x>1;由g′(x)<0可得-2<x<1,
∴x=-2时,函数取得极大值10;
(2)设切点为(a,b),则
∵y=x[f(x)-
x-6]=x3-12x,
∴y′=3x2-12,
∴过点A(2,-24)的切线方程为y+24=(x-2)(3a2-12)
将(a,b)代入,化简可得2a3-6a2=0,
∴a=0或a=3,
∴切线方程为y=-12或y=15x-54.
由g′(x)>0可得x<-2或x>1;由g′(x)<0可得-2<x<1,
∴x=-2时,函数取得极大值10;
(2)设切点为(a,b),则
∵y=x[f(x)-
| 3 |
| 2 |
∴y′=3x2-12,
∴过点A(2,-24)的切线方程为y+24=(x-2)(3a2-12)
将(a,b)代入,化简可得2a3-6a2=0,
∴a=0或a=3,
∴切线方程为y=-12或y=15x-54.
点评:此题考查学生会利用导数研究曲线上某点的切线方程,是一道综合题.学生在解决此类问题一定要分清“在某点处的切线”,还是“过某点的切线”;同时解决“过某点的切线”问题,一般是设出切点坐标解决.

练习册系列答案
相关题目
双曲线的一个顶点为(2,0),一条渐近线方程为y=
x,则该双曲线的方程是( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
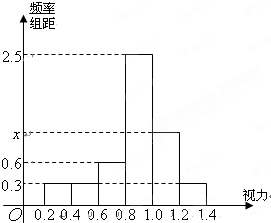 为了解某校高三学生的视力情况,随机抽查了该校50名高三学生,得到如图所示的频率分布直方图.
为了解某校高三学生的视力情况,随机抽查了该校50名高三学生,得到如图所示的频率分布直方图.