题目内容
在空间直角坐标系中,点P(1,-2,3)关于坐标平面xOz对称的点Q的坐标为 .
考点:空间中的点的坐标
专题:空间位置关系与距离
分析:根据空间直角坐标系中点两点关于坐标平面对称的规律,可得与点P(1,-2,3)关于平面xoz的对称点,它的横坐标和竖坐标与P相等,而纵坐标与P互为相反数,因此不难得到正确答案.
解答:
解:设所求的点为Q(x,y,z),
∵点Q(x,y,z)与点P(1,-2,3)关于平面xoz的对称,
∴P、Q两点的横坐标和竖坐标相等,而纵坐标互为相反数,
即x=1,y=2,z=3,得Q坐标为(1,2,3)
故答案为:(1,2,3).
∵点Q(x,y,z)与点P(1,-2,3)关于平面xoz的对称,
∴P、Q两点的横坐标和竖坐标相等,而纵坐标互为相反数,
即x=1,y=2,z=3,得Q坐标为(1,2,3)
故答案为:(1,2,3).
点评:本题借助于两点关于一个平面对称,已知其中一点坐标的情况下求另一点的坐标,考查了空间点与点关于平面对称的知识点,属于基础题.

练习册系列答案
相关题目
为了得到函数y=
(sin2x-cos2x)的图象,只要把函数y=sin2x的图象上所有的点( )
| ||
| 2 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
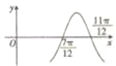
已知函数f(x)=cos(ωx+φ)(ω>0,|φ|≤
)的图象如图所示,则φ等于( )
| π |
| 2 |

A、
| ||
B、
| ||
C、-
| ||
D、-
|