题目内容
已知函数f(x+1)=f(x-1),当0≤x≤1时,f(x)=2x-1,则f(112.5)= .
考点:函数的周期性
专题:函数的性质及应用
分析:首先求证函数 f(x)为周期函数,并求出其周期,然后根据条件求得即可.
解答:
解:∵f(x+1)=f(x-1),
∴f(x+1+1)=f(x+1-1)
∴f(x+2)=f(x),
∴f(x) 是周期为2的周期函数.
当0≤x≤1时,f(x)=2x-1,
f(0.5)=2×0.5-1=0,
∴f(112.5)=(56×2+0.5)=f(0.5)=0.
故答案为:0.
∴f(x+1+1)=f(x+1-1)
∴f(x+2)=f(x),
∴f(x) 是周期为2的周期函数.
当0≤x≤1时,f(x)=2x-1,
f(0.5)=2×0.5-1=0,
∴f(112.5)=(56×2+0.5)=f(0.5)=0.
故答案为:0.
点评:本题考查了函数的周期性,属于基础题.

练习册系列答案
相关题目
若“0<x<1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则a的取值范围是( )
| A、(-∞,0]∪[1,+∞) |
| B、(-1,0) |
| C、[-1,0] |
| D、(-∞,-1]∪[0,+∞) |
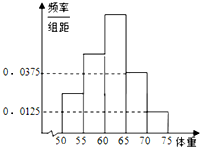 为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是
为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是 某校高三年级从一次模拟考试中随机抽取50名学生(男、女生各25名),将数学成绩进行统计,所得数据的茎叶图如图所示,以组距为10将数据按[80,90),[90,100),…,[130,140),[140,150]分成七组绘制频率分布直方图,则落在区间[130,140)的小矩形的面积为( )
某校高三年级从一次模拟考试中随机抽取50名学生(男、女生各25名),将数学成绩进行统计,所得数据的茎叶图如图所示,以组距为10将数据按[80,90),[90,100),…,[130,140),[140,150]分成七组绘制频率分布直方图,则落在区间[130,140)的小矩形的面积为( )