题目内容
已知sinx+cosx=
,求sin4x+cos4x的值.
| 2 |
| 3 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:将已知等式两边平方,利用同角三角函数间基本关系求出sinxcosx的值,原式利用完全平方公式及同角三角函数间基本关系化简,将sinxcosx的值代入计算即可求出值.
解答:
解:将sinx+cosx=
,两边平方得:(sinx+cosx)2=1+2sinxcosx=
,
∴sinxcosx=-
,
则sin4x+cos4x=(sin2x+cos2x)2-2sin2xcos2x=1-2sin2xcos2x=1-2×
=
=
.
| 2 |
| 3 |
| 4 |
| 9 |
∴sinxcosx=-
| 5 |
| 18 |
则sin4x+cos4x=(sin2x+cos2x)2-2sin2xcos2x=1-2sin2xcos2x=1-2×
| 25 |
| 18×18 |
| 274 |
| 324 |
| 137 |
| 162 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
集合A={x|x2>1},B={x|x+a≥0},若∁UA⊆B,则实数a的取值范围是( )
| A、[-1,+∞) |
| B、[1,+∞) |
| C、(-∞,1] |
| D、(-∞,-1] |
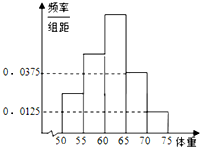 为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是
为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为15,则抽取的男生总人数是