题目内容
讨论f(x)=2x•|log0.5x|-1的零点个数.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:通过令f(x)=0,将方程的解转化为函数图象的交点问题,从而判断函数的零点个数.
解答:
解:函数f(x)=2x|log0.5x|-1,令f(x)=0,
则2x|log0.5x|=1,
即(
)x=|log0.5x|,
在同一坐标系中作出y=(
)x.与y=|log0.5x|,如图,

由图可得零点的个数为2.
则2x|log0.5x|=1,
即(
| 1 |
| 2 |
在同一坐标系中作出y=(
| 1 |
| 2 |

由图可得零点的个数为2.
点评:本题考查函数的零点,函数的图象的作法,考查数形结合与转化思想.

练习册系列答案
相关题目
若(1+x)m+(1+x)n展开式中x项的系数是12,则x2系数的最小值是( )
| A、11 | B、25 | C、30 | D、45 |
函数f(x)=3x+x-2的零点所在的区间是( )
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,3) |
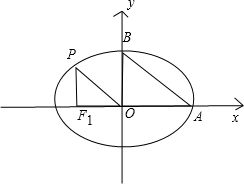 如图,从椭圆
如图,从椭圆