Question

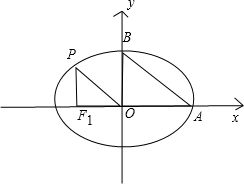如图，从椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）上一点P作x轴的垂线，恰好通过椭圆的一个焦点F₁，椭圆与x轴交于点A，与y轴交于点B，所确定的直线AB与OP平行，求

c

a

的值．

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：由

c2

a2

+

y2

b2

=1，解得：y=

b2

a

，由AB∥OP得：

a

b

=

ac

b2

，从而求出答案．

解答： 解：由题意得：F₁（-c，0），
不妨设P（-c，y），代入椭圆的方程得：

c2

a2

+

y2

b2

=1，解得：y=

b2

a

，
由AB∥OP得：

a

b

=

ac

b2

，
∴b=c=

2

2

a，
∴

c

a

=

2

2

．

点评：本题考查了椭圆的性质，考查了直线平行的性质，是一道基础题．