题目内容
若(1+x)m+(1+x)n展开式中x项的系数是12,则x2系数的最小值是( )
| A、11 | B、25 | C、30 | D、45 |
考点:二项式定理的应用
专题:计算题,不等式的解法及应用,二项式定理
分析:利用二项式定理求出展开式中x项系数为m+n=12,含x2项系数为
,再利用基本不等式求出其最小值即可.
| m2-m+n2-n |
| 2 |
解答:
解:f(x)=1+Cm1x+Cm2x2+…Cmmxm+1+Cn1x+Cn2x2+…+Cnnxn
=2+(m+n)x+
x2+…,
由已知,m+n=11,
由m2+n2≥2mn,得2m2+2n2≥m2+n2+2mn=(m+n)2=144,
于是 m2+n2≥72.
所以含x2项系数
=
≥
=30.
故选:C.
=2+(m+n)x+
| m2-m+n2-n |
| 2 |
由已知,m+n=11,
由m2+n2≥2mn,得2m2+2n2≥m2+n2+2mn=(m+n)2=144,
于是 m2+n2≥72.
所以含x2项系数
| m2-m+n2-n |
| 2 |
| m2+n2-12 |
| 2 |
| 72-12 |
| 2 |
故选:C.
点评:本题考查二项式定理,基本不等式求最值.考查计算、配凑转化的能力.

练习册系列答案
相关题目
函数y=
-
+3的定义域是( )
| 5-x |
| x+2 |
| A、-2≤x≤5 |
| B、-5≤x≤2 |
| C、{-2,5} |
| D、{x|-2≤x≤5} |
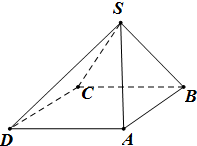 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠ABC=45°,AB=2,BC=2