题目内容
10.函数y=$\sqrt{3}$cos2x-sin2x的一个单调区间是( )| A. | [-$\frac{π}{6}$,$\frac{π}{6}$] | B. | [-$\frac{π}{6}$,$\frac{2π}{3}$] | C. | [$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{π}{12}$,$\frac{5π}{12}$] |
分析 由三角函数公式可得y=2cos(2x+$\frac{π}{6}$),由整体法可得函数的单调区间,结合选项可得.
解答 解:由三角函数公式可得y=$\sqrt{3}$cos2x-sin2x
=2($\frac{\sqrt{3}}{2}$cos2x-$\frac{1}{2}$sin2x)=2cos(2x+$\frac{π}{6}$),
令2kπ≤2x+$\frac{π}{6}$≤2kπ+π可解得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,
故函数的单调递减区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z,
同理可得函数的单调递增区间为[kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z,
结合选项可得[-$\frac{π}{12}$,$\frac{5π}{12}$]为函数的一个单调递减区间.
故选:D.
点评 本题考查两角和与差的三角函数公式,涉及函数的单调性,属基础题.

练习册系列答案
相关题目
20.已知tanα=2,α为第一象限角,则sin2α+cosα的值为( )
| A. | $\sqrt{5}$ | B. | $\frac{{4+2\sqrt{5}}}{5}$ | C. | $\frac{{4+\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}-2}}{5}$ |
1.若直线x+my-1=0与不等式组$\left\{\begin{array}{l}{x+2y-4≤0}\\{x-y+2≤0}\\{x≥-1}\end{array}\right.$,表示的平面区域有公共点,则实数m的取值范围是( )
| A. | [$\frac{1}{2}$,2] | B. | [$\frac{1}{3}$,3] | C. | (-∞,$\frac{1}{3}$]∪[3,+∞) | D. | (-∞,$\frac{1}{2}$]∪[2,+∞) |
2. 如图,若在矩阵OABC中随机撒一粒豆子,则豆子落在图中阴影部分的概率为( )
如图,若在矩阵OABC中随机撒一粒豆子,则豆子落在图中阴影部分的概率为( )
 如图,若在矩阵OABC中随机撒一粒豆子,则豆子落在图中阴影部分的概率为( )
如图,若在矩阵OABC中随机撒一粒豆子,则豆子落在图中阴影部分的概率为( )| A. | 1-$\frac{2}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{2}{{π}^{2}}$ | D. | 1-$\frac{2}{{π}^{2}}$ |
19.若f(tanx)=sin2x,则f(-1)的值是( )
| A. | -sin2 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
20.已知z=($\frac{1-i}{\sqrt{2}}$)2016(i是虚数单位),则z等于( )
| A. | -1 | B. | 1 | C. | 0 | D. | i |
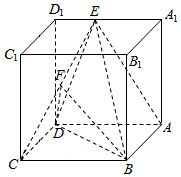 如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.
如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.